Image in a Plane Mirror: Let consider a point object A placed in front of a plane mirror M as shown in the Figure. Consider a ray of light AO from the point object incident on the mirror and reflected along OB. Draw the normal ON to the mirror at O.
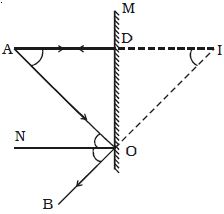
The angle of incidence AON = angle of reflection BON
Another ray AD incident normally on the mirror at D is reflected back along DA. When BO and AD are produced backwards, they meet at I. Thus the rays reflected from M appear to come from a point I behind the mirror. From the figure;
Angle AON = Angle DAO, alternate angles and Angle BON = Angle DIO, corresponding angles it follows that Angle DAO = Angle DIO.
The triangles ODA and ODI are congruent.
So, AD = ID
For a given position of the object, A and D are fixed points. Since AD = ID, the point I is also fixed. It should be noted that AO = OI. So the object and its image in a plane mirror are at equal perpendicular distances from the mirror.