Derivation of Equations of motion with the help of graphs
(a) Graph in case of the equation, v = v0 + at
In this equation, there are two variables— one is t and the other one is v. A graph is drawn taking t on the X-axis and v on the Y-axis [Fig]. In the figure, normal PN is drawn from point P to Y-axis. Let consider that the final velocity at time t = v = OY. Now OY = OA + AY i.e., v = v0 + at.
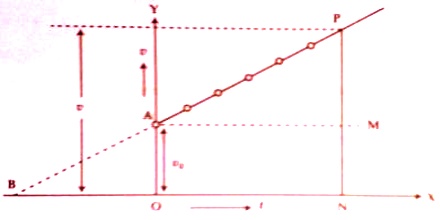
Here, slope, a = PM/AM = AY/AM = AY/t
The equation v = v0 + at is obtained from the graph.
In case of motion of a body from rest, v0 = 0, a = constant.
So, v = 0 + constant x t
so, v ∞ t
That means, velocity is proportional to time.
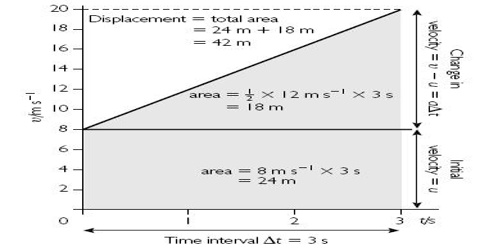
(b) Graph for the equation, s = v0t + ½ at2
In figure, graph of ‘v’ versus ‘t’ is a straight line.
In the figure PN ┴ OX; AM ┴ PN.
Let initial velocity = v0, uniform acceleration = a, ON = t and distance travelled in time t = s.
Now, s = Area of OAPN
= area of the rectangle OAMN + area of the triangle AMP
= OA x ON + ½ AM PM
= v0t + ½ AM PM
Again, slope ‘a’ PM/AM = PM/t
so, PM = at
and, s = v0t + ½ t.at = v0t + ½ at2
So, the equation can be presented in graph.
In case of a body moving with uniform acceleration from rest, then,
s = 0 x t + ½ constant x t2
or, s = constant x t2
or, s ∞ t2
That means, displacement is proportional to time.