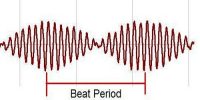
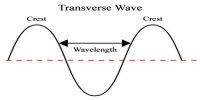
The number of degrees of freedom of a dynamical system is defined as the total number of co-ordinates or independent variables required to describe the position and configuration of the system.
For translatory motion
(i) A particle moving in a straight line along any one of the axes has one degree of freedom (e.g) Bob of an oscillating simple pendulum.
(ii) A particle moving in a plane (X and Y axes) has two degrees of freedom. (eg) An ant that moves on a floor.
(iii) A particle moving in space (X, Y and Z axes) has three degrees of freedom. (eg) a bird that flies.
A point mass cannot undergo rotation, but only translatory motion. A rigid body with finite mass has both rotatory and translatory motion. The rotatory motion also can have three co-ordinates in space, like translatory motion; Therefore a rigid body will have six degrees of freedom ; three due to translatory motion and three due to rotatory motion.