Superposition of waves: The principle of superposition may be applied to waves whenever two (or more) waves travelling through the same medium at the similar time. When two sound waves cross at the same time a particle of a medium, that particle is excited due to the combined effect of the two waves. The resultant at the displacement of the particle at any instant is equal to the vector sum of displacement of individual waves. It is called superposition of waves.
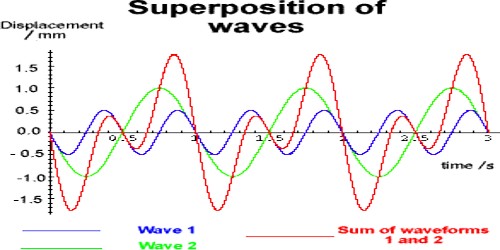
The waves pass through each other without being troubled. The net disarticulation of the medium at any point in space or time, is basically the sum of the individual wave displacements. This is true of waves which are finite in length (wave pulses) or which are continuous sine waves.
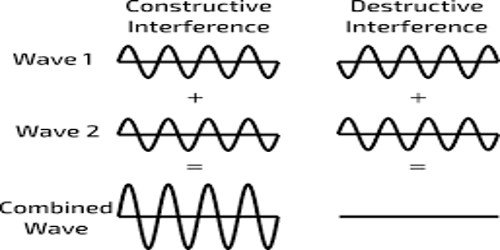
Interference of sound: When two waves of same frequency travelling in the same direction in a medium superpose with each other, their resultant intensity is maximum at some points and minimum at some other points. This phenomenon of superposition is called interference.
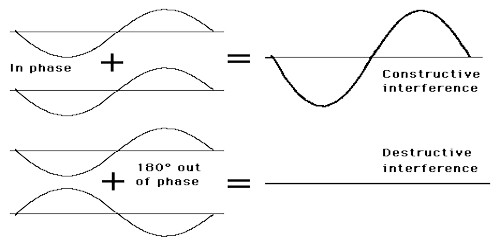
If a strong or faint sound is heard due to the superposition of two sound waves of equal frequency and wavelength, then the phenomenon is called interference of sound.