Characteristic of force for simple harmonic motion:
If the acceleration of an oscillating particle is proportional to distance from its equilibrium position and always towards the equilibrium position, then that motion of the particle is called simple harmonic motion. Its function is one which is always related to the smoothest circular motion or its projections where all its higher integrals and derivatives have a comparable smooth function each oriented by 90 degrees with respect to one another.
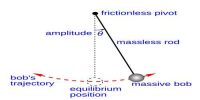
(i) A restoring force must act on the body. It is a special type of force acting on a particle having simple harmonic motion.
(ii) In case of this motion acceleration of the particle and magnitude of the force acting on it is proportional to the displacement. The body must have acceleration in a course opposite to the dislocation and the acceleration must be directly proportional to displacement.
(iii) The direction of the acceleration and force acting on the particle always remains towards the equilibrium, i.e., in the opposite direction of displacement. The acceleration ‘a’ of the body is directly proportional to the displacement ‘x’ and is always towards the equilibrium position. The acceleration is directly proportional to its displacement from the mean position and is always directed towards it (a ∝ −ω2x)
(iv) The system must have inertia (mass). The body must be elastic. The frictional forces are small enough to be ignored.
(v) Direction of force in this type of motion is linear. It is a particular case of periodic motion. It is a motion along a straight line.
(vi) It is a type of oscillatory motion. It must consist of an ample amount restoring force to pull it back after deformation.
Simple Harmonic Motion (SHM) is a restoring force that must act on the body. The body moves back and forth with respect to a mean position. The body must have acceleration in a direction opposite to the displacement and the acceleration must be directly proportional to displacement. The body returns to a given point in the path with the same velocity after regular intervals of time. The force acting on the body always tries to bring it back to its equilibrium position.
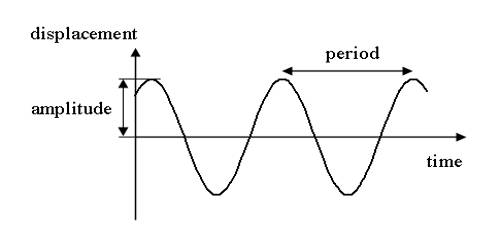
Obviously, all the periodic motions do not have those characteristics. The maximum displacements on either side of the equilibrium position are equal. So, all simple harmonic motions are periodic motions but all periodic motions are not simple harmonic motions.