Applications of Newton’s Laws of Motion
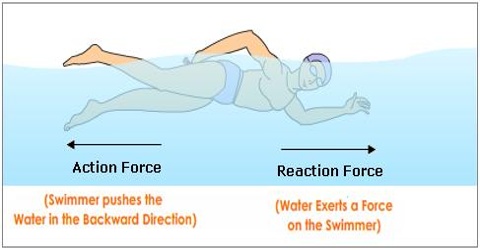
When a body applies force on another body then the second body also applies equal and opposite force on the first body. We have learnt about this action and reaction forces from Newton’s third law of motion. In nature forces act in couples. In nature there is not individual separate force. Two forces are complementary to each other. One of these forces is called action force and the other one is reaction force. As long as action force is there, there exists reaction force also. Practical application of Newton’s laws of motion are described below with example.
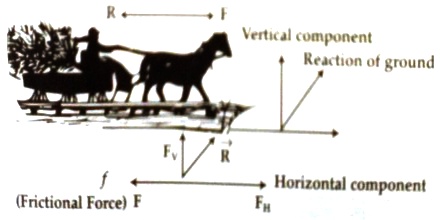
Motion of a carriage: When a carriage moves on the road, then force F applied in the belt on the shoulder of the horse or on the arms moves the carriage forward; at the same time carriage also pulls the horse backward with equal and opposite force F. Naturally, quastion arises how the carriage moves forward? Look at the picture below,
How the carriage moves forward with passengers?
In order to move the carriage the horse applies force on the ground obliquely. Simultaneously ground also applies equal and opposite reaction force R on the horse. This force can be resolved into horizontal FH and vertical FV components. Vertical components FV, balances weight of the horse. Now if the horizontal component FH becomes greater than reaction force R applied backward by the carriage, then due to the action of the FH – R horse moves forward i.e., the carriage moves ahead (Figure).
Now if the motion of the carriage is considered separately, then we will find that two forces act on it-
(i) Frictional force ‘f’ on the wheel due to its contact with the ground. This force resists the motion of the carriage.
(ii) Force applied by the horse F; this force tries to pull the carriage ahead. When the value of F is greater than ‘f’, then only due to the action of the force F – f, the carriage moves forward.
Now if the carriage along with passengers moves with uniform speed i.e., acceleration becomes zero, then according to the first law of motion net force acting becomes zero. So, FH – F = 0 and F – f = 0 i.e., F = FH – f. If the carnage along with passengers moves with acceleration, then acceleration of the horse will be (FH – F)/M and acceleration of the carriage will be (F – f)/MR here M and MR are respectively masses of the horse and the carriage. The two forces FH and f are self-controlled force and their magnitudes are controlled in such a way that acceleration of the carnage and the horse becomes equal. So, the horse and the carnage move ahead simultaneously.