The concept of the laws Current and resistance in a simple circuit can be determined by using Ohm’s law. But if the circuit is complex then Ohm’s law is not sufficient. For this reason, Kirchhoff’s two laws are used to calculate current and resistance in a complex circuit.
Kirchoff’s Law in parallel combination of electric cells
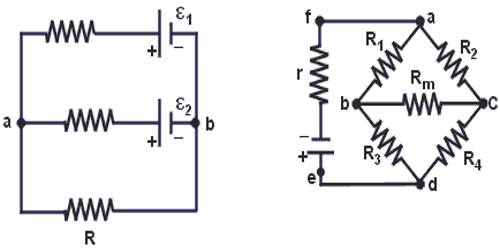
In this combination, positive terminals of all the cells are connected at one point and negative terminals at another point. The figure shown such cells connected in parallel across some external resistance R. Let e.m.f and internal resistance of each cell are E and r respectively.
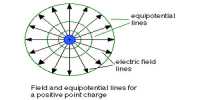
Suppose, A, B and C are three electric cells. Their electromotive forces are E1, E2, E3, respectively and their internal resistances are r1, r2, r3. Connecting these cells in parallel their terminals are connected across in a resistance in parallel combination. Let the currents flowing through the cells E1, E2, E3 be repetitively i1, i2, i3.
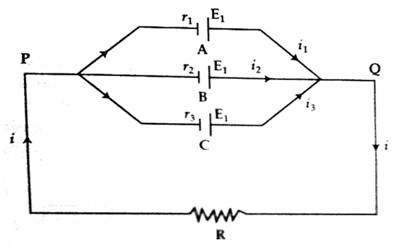
Now applying Kirchoff’s law at points P and Q we get,
i1 + i2 + i3 = i
Applying Kirchoff s second law,
from the circuit PAQRP. We get, i1R1 + iR = E1 … … … (1)
from the circuit PBQRP, i2R2 + iR = E2 … … … (2)
from the circuit PCQRP, i3R3 + iR = E3 … … … (3)
Equations (1), (2) and (3), are divided by r1, r2, r3 respectively and adding the results we get,
(i1 + i2 + i3) + i (R/r1 + R/r2 + R/r3) = E1/R1 + E2/R2 + E3/R3
or, i + i (R/r1 + R/r2 + R/r3) = E1/R1 + E2/R2 + E3/R3
or, i { 1 + R (1/r1 + 1/r2 + 1/r3)} = E1/R1 + E2/R2 + E3/R3
So, i = [E1/R1 + E2/R2 + E3/R3] / [1 + R (1/r1 + 1/r2 + 1/r3)]
Now by inserting the values of R, r1 + r2 + r3 and E1 + E2 + E3 the value of ‘i’ can be determined. If the electromotive force of each of the cells is E and internal resistance r, then
i = (nE/r) / [1 + (nR/r)] = nE / (nR + r)
Potential difference: Potential difference between the terminals of R is,
V = iR = [nE / (nR+ r) x R]