The concept of the laws Current and resistance in a simple circuit can be determined by using Ohm’s law. But if the circuit is complex then Ohm’s law is not sufficient. For this reason, Kirchhoff’s two laws are used to calculate current and resistance in a complex circuit.
Kirchoff’s Law in case of series combination of cells
In this combination, cells are so connected that -ve terminal of each cell is connected with the +ve terminal of next and so on. Suppose n cells are connected in this way. Let e.m.f and internal resistance of each cell are E and r respectively.
Net e.m.f of the cells = nE
Total internal resistance = nr
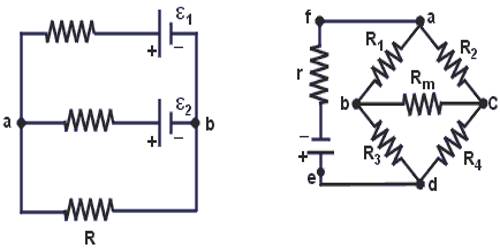
Determination of current: Suppose there are three electric cells. Their electromotive forces are E1, E2, E3 and internal resistances are r1, r2, r3 respectively [Figure]. These are connected with a resistor R in series. Let the current in the circuit be ‘i’.
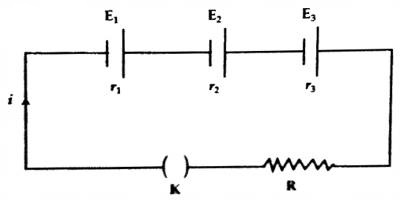
Applying Kirchoff’s second law in the said circuit we get,
E1 + E2 + E3 = ir1 + ir2 + ir3 + iR
or, i (r1 + r2 + r3 + R) = E1 + E2 + E3
So, i = (E1 + E2 + E3) / (r1 + r2 + r3 + R) … …. … (3.21)
If ‘n’ number of cells are connected similarly, then,
i = (E1 + E2 + E3 … … + En) / (R+ r1 + r2 + r3 … … + rn)
If the electromotive force of each cell is E and its internal resistance is r, then,
i = nE / (R + nr)
Determination of potential difference: Potential difference between the resistor R for the flow of current ‘i’ through it is –
V = iR = nER / (R + nr)