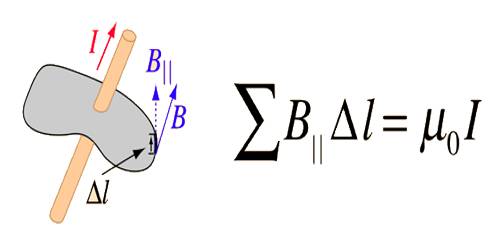Application of Ampere’s Law
“The line integral of a magnetic field along a closed path is equal to μ0 times, the current flowing through the area subtended by that path.”
This law states that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop.
Explanation: Suppose, current is flowing through a conductor. If a magnetic needle is placed in the magnetic field produced due to the flow of current it will be displaced from the equilibrium position. But in order to deflect the needle from its equilibrium position, a torque will act on it. Magnitude of this torque is,
τ = p x B
or, pB Sinθ
Here, p = magnetic moment of the magnetic needle,
B = magnitude of the magnetic field
and θ = angle between p and B.
For any magnetic bar, p is constant.
So, τ ∞ B
If currents of different values are allowed to flow through the wire and the magnitude of B at different distances from the wire are determined, then it will be seen that the magnetic field B varies proportionally with a current ‘i’ and inversely proportional to distance r.
So, B = i/r
or, B = constant x (i/r) … … … (2)
If this constant is taken as μ0/2π then the equation (2) becomes correct. So, the value of this constant must be taken as (μ0/2π), here μ0 = permeability of the medium. Its value is 4π x 10-7 WbA-1m-1.
So, from equation (2) we get,
B = (μ0/2π) x (i/r) = (μ0/2πr) x i … … … (3)
According to equation (3), B(2πr) = μ0i … … … (4)
But 2πr is the circumference of a circle of radius r. Again, the magnitude of B at all points on the circumference of that circle is same (Figure) and the direction of B at each point is along the tangent drawn at that point. So, at each point, the value of the angle between B and small element on the circumference of the circle is zero.
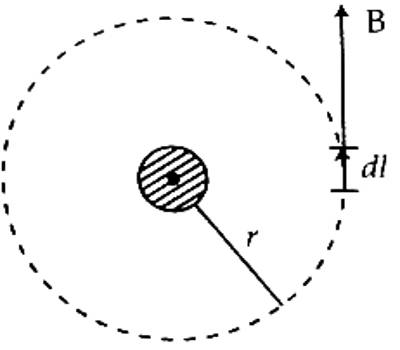
The left-hand side of the equation (4) can be expressed as §B.dl.
Here, dl = displacement vector of the path difference.
Then, we get, §B.dl = μ0i.
It is the Ampere’s law. It has been seen by different experiments that the above law is true for any magnetic field, current flow, and integral path.