Scottish theoretical physicist James Clerk Maxwell (1831-1879) unified electricity and mag-netism into classical electrodynamics. A logical development of his equations follows. In going from electrostatics (Δ x E = 0) to electrodynamics, E is no longer conservative, and Δ x E is given instead by Faraday’s law. In a similar way, Ampere’s law needs modifying. To show this, consider the second-derivative Δ • (Δ x a) which must be zero for any vector field a(r). Substitution shows that E(r) satisfies this condition in electrodynamics, but that B(r) does not unless Ampere’s law is modified.
The divergence of Ampere’s law
Δ • (Δ x v) = Δ (μ0 J)
is non-zero in electrodynamics because charge conservation requires that
Δ . J = – (ϐp / ϐt)
We can gain further insight to the problem by considering the charging a capacitor as in below Figure. Ampere’s law in integral form
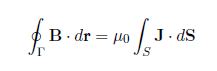
should apply for any surface S bounded by closed loop Г, such as surfaces S1, S or S3. The right hand side is μ0I for surfaces S1 and S3, but is zero for surface S2 which goes between the capacitor plates.
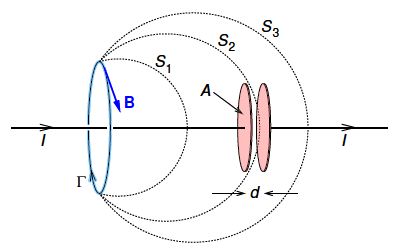
Figure: The problem with Ampere’s law as illustrated by the charging of a parallel plate capacitor.