Consider a monochromatic plane EM wave incident on a plane boundary between two dielectric materials. Part of the wave is transmitted and part is reflected. Prom symmetry arguments, the reflected and transmitted rays must be in the same plane as the incident ray and the normal to the boundary. This plane is called the plane of incidence. Below Figure shows the ray geometry in the plane of incidence.
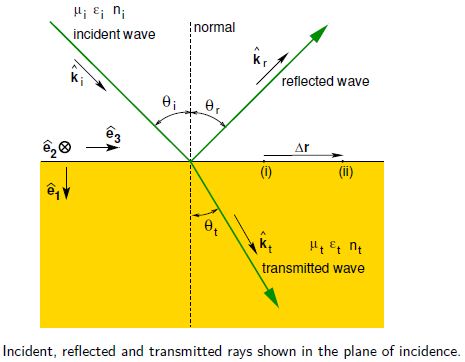
We use subscripts i, r and t to refer to quantities related to the incident, reflected and transmit-ted waves, respectively. We also use subscript i to indicate the material in which the incident wave (and reflected wave) propagates, and subscript t to indicate the material in which the transmitted wave propagates.
The electric and magnetic fields of the incident, reflected and transmitted waves are
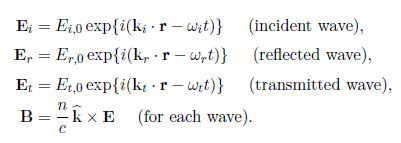
The electromagnetic field must satisfy the boundary conditions for E, D, B and H at every point on the interface between the two materials at all times. For the boundary conditions to hold at all times, to must be the same for all three waves.
For the boundary conditions to be satisfied at every point, e.g. simultaneously at points “(i)” and “(ii)” in above Figure,
ki • Δ r = kr • Δ r = kt * Δ r. …….(1)
so, ki sin θi = kr sin θr = kt sin θt … ….(2)
Since ki = kr because the incident and reflected waves propagate in the same medium, we have
Θi = θr (law of reflection)
Similarly, since k = w/ vp= wn/c and w is the same for all waves,
Ni sin θi = nt sin θt (law of refraction or “Snell’s Law”)
We now know what the directions of the reflected and transmitted waves are, but how much of the incident intensity is reflected or transmitted? The reflectance, R, also known as the reflectivity, is the fraction of the incident power that is reflected. The transmittance, T, also known as the transmissivity, is the fraction of the incident power that is transmitted. We shall see that the reflectance and transmittance are different if the orientation of the plane of polarisation with respect to the plane of incidence, is parallel or perpendicular to the plane of incidence.
In general, the incident wave can be treated as a superposition of two linearly polarised waves whose planes of polarisation are orthogonal, with one wave polarised parallel to, and the other perpendicular to, the plane of incidence in Laws of Reflection. This is equivalent in quantum mechanics to the wave function being a superposition of eigenstates of the system.