Since for an EM wave B = √(μƐ) E, the electric and magnetic contributions to energy density are equal,
(Ɛ E2)/2 = B2/2μ
and so the total energy density in the Electromagnetic waves are
u = [ (Ɛ E2)/2 + B2/2μ ] = Ɛ E2 = B2/μ
so, u (r, t) = Ɛ E02 cos2 (k*r – ωt + ϐ)
The energy flux is given by the Poynting vector S = E x H, and for EM waves in a linear non-dispersive medium this is
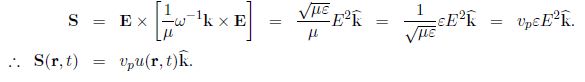
The intensity (W m-2) of the wave is the time-average of the magnitude of the Poynting vector
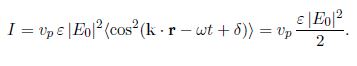
Since the momentum density is g = S/c2, the momentum flux of an EM wave is vp g. Its magnitude is just the amount of momentum crossing unit area of a surface perpendicular to K per unit time, and we may use it to find the radiation pressure. If a parallel beam of radiation is perfectly absorbed then the radiation pressure is
Prad, abs = (vp/C2) S = (vp2 /C2) u
whereas if the radiation is perfectly reflected then the radiation pressure is twice as large.
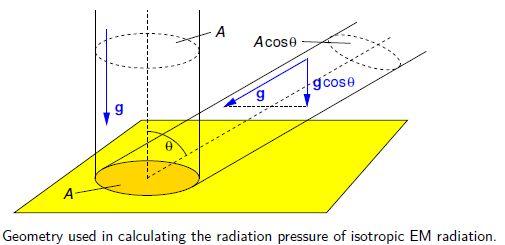
To obtain the radiation pressure of isotropic radiation we need to integrate the momentum flux incident on area A of one side of a plane surface, taking only the component of momentum density perpendicular to the plane, i.e. g cos θ, and the projected area A cos θ in below figure,
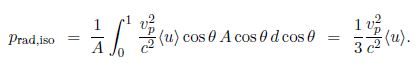
Note that the radiation pressure in empty space is p = u/3, and this is the equation of state of a photon gas.