Some chemical reactions may have come to an equilibrium,
A +2B ≈ 3C+2D
At a given temperature this reaction will eventually come to equilibrium, the double 1 that both the forward reaction and the reverse reaction are still occurring simultam of the forward and reverse reactions have become equal at chemical equilibrium. Once the n equilibrium the concentrations of the reactants and products are then constant am another by the reaction’s equilibrium constant Kc which is characteristic of the reaction For solutions, the concentrations (e.g. c) are conventionally written as a pure number: symbol in square brackets, e.g. [A], times the units of mol L-1.
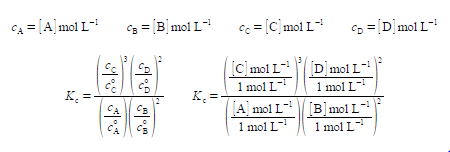
In the equation for Kc each concentration is divided by its own standard state concentration. We use as the symbol for standard state a superscript degree which is pronounced as “naught”, “zero” or “standard”. For solutes, the standard state concentration are e.g. c°A = 1 mol L-1. The units will cancel out to give the pure number “dimensionless concentrations” e.g. [A]. So Kc the equilibrium constant must also be dimensionless. In chemical equilibria each of the concentrations is raised to the same power as its stoichiometric coefficient.
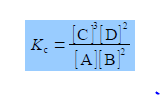
Firstly, for the above equilibrium reaction calculate the value of the equilibrium constant Kc in a solution where all four of the concentrations are equal to 0.1 mol L-1.
Secondly, calculate the new concentration of [C] if we alter the concentrations to [A] = 0.2 mol L-1, [B] = 0.15 mol L-1 and [D] = 0.25 mol L-1 ?
Solution
Firstly, we need to find the value for the chemical equilibrium constant,
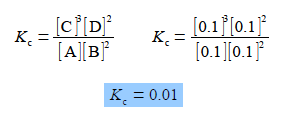
Secondly, we rearrange the equilibrium constant equation so that [C] is the subject of the equation. This is done sequentially by: (1) multiplying both sides of the equation by [A] [B]2; (2) and then cancelling out top and bottom within any single term;
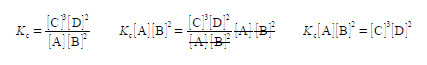
(3) then dividing by [D]2 on both sides of the equation and cancelling top and bottom within any single term;
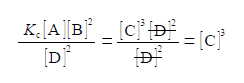
(4) writing [C]3 as the subject; (5) substituting in the physical quantities; and (6) taking the cube root of [C]3 gives the concentration of molecule C.
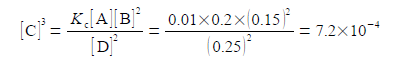
As [C] is the symbol for the pure number of the concentration, so the concentration in mol L-1 is
[C] = 8.96 x 10-2 Cc = C mol L-1
Increasing the concentrations of [A], [B] and [D] has decreased the concentrations of [C] in order to maintain the equilibrium constant Kc at a constant value.











