By definition, for external reflection nt > ni. Hence, √ [(nt / ni)2 – sin2 θi] is real for all θi, and so therefore are r┴ , t┴, r‖ and T‖ plotted in Fig (a) for light incident from air (ni ≈ 1) on to flint glass (ni ≈ 1.62).
Notice that for the example in Fig (a) as the angle of incidence varies from θi = 0° to 90° that the amplitude reflection coefficient for parallel polarisation changes smoothly from r‖ = + 0.24 to —1. The angle of incidence at which the amplitude reflection coefficient for parallel polarisation is zero is called Brewster’s angle θB, i.e. r‖ (θB) = 0. At Brewster’s angle only perpendicular polarised waves are reflected, and this is one method of producing linearly polarised light. We may obtain Brewster’s angle by setting r‖ = 0 in next Equation to obtain
Cos θB = 1 / √(1 + (nt / ni)2
Tan θB = nt / ni
The amplitude reflection coefficients are in general complex, but in the case of external reflection r‖ and r┴ are real for all θi. If r > 0 the phase shift is zero, but if r < 0 there is a phase shift on reflection by π radians (180°) since e+iπ = —1. This is illustrated in Fig (b).
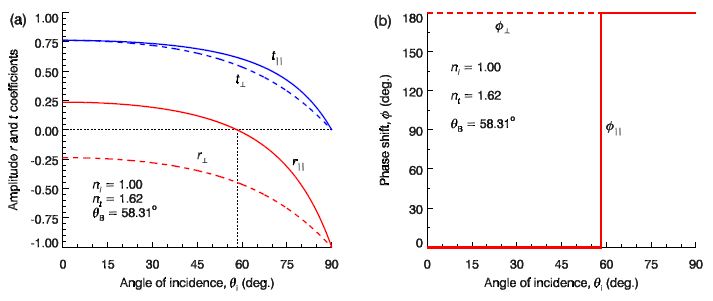
Figure: Amplitude reflection and transmission coefficients (a) and phase shift (b) for external reflection off flint glass.












