Momentum can be transferred when a driving force in the form of a velocity difference exists. Transport of Momentum can be explained by describing the situation sketched in below Figure, which shows an example of molecular Transport of Momentum.
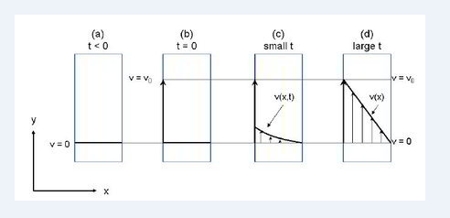
One plate to the left and one plate to the right are separated by a Newtonian.
(a) The velocity of both plates is zero.
(b) At t= 0 the left plate is set at motion with a constant velocity vo while the right plate is kept at rest
(c) The fluid just next to the moving plate start to move. This fluid in motion then starts to move the fluid to the right which is at rest. Thus as the velocity is propagated, momentum is transferred in the x direction. At small values of t, the velocity in the fluid between the plates is a function of both time and distance x.
(d) At large values of t, steady state is established and a linear velocity profile in the fluid is reached. Thus at steady state the velocity is only a function of the distance x in the fluid.
A Newtonian fluid (the term Newtonian will be explained in a moment) is contained between two plates. It could be water or ethanol for example. Initially the plates and the fluid are a rest. At time t = 0 the plate to the left is suddenly set at motion with a constant velocity v0 it the y-direction. The fluid just next to the left plate will then also start to move in the y-direction. That way the fluid throughout the whole distance between the plates will eventually be set at motion. The right plate is kept at rest. The fluid just next to the right plate will all the time not move because “no slip” is assumed between the fluid an the plate. At small values of t the velocity in the y-direction is a function of both the time and distance x in the fluid. After a while a linear steady state velocity profile is established and thus the velocity in the y-direction is only a function of the distance x in the fluid.
A constant force is required to keep the left plate at motion. This force is proportional to the velocity vo, the area of the plate and inversely proportional to the distance between the two plates. The force pr. area ration can be thought of as a flux of y-momentum (momentum in the y-direction) in the x-direction. The proportionality constant is the dynamic viscosity μ of the fluid (the dynamic viscosity can also be denoted with the symbol μ). The viscosity of a fluid is then associated with a resistance towards flow.
At steady state the momentum flux (force in y-direction pr. area) through the fluid is given by the flux equation, which is called Newton’s law of viscosity:
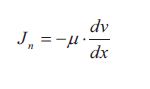
Above equation only applies to fluids with molecular weights less than about 5000. Such fluids are called Newtonian fluids because they are described by Newton’s law of viscosity. The viscosity of such fluids is independent of the velocity gradient which is not the case for non-Newtonian fluids.
The flux J„ is the flux of y-momentum in the direction x through the fluid. The gradient dv/dx is the velocity gradient which is the driving force. Remember that the velocity is in the y-direction and the momentum flux is in the x-direction. This gradient is often referred to as the shear rate. The term p is as mentioned earlier the dynamic viscosity of the fluid. The value of the dynamic viscosity together with density of the fluid determines how fast the linear steady state velocity profile develops. The dynamic viscosity and the density of the fluid can together be expressed at the kinematic viscosity v:
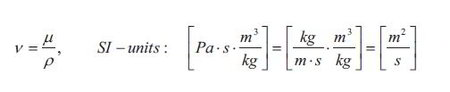
It is seen form above equation that the kinematic viscosity has the same units as the ordinary diffusivity D and the thermal diffusivity α. Thus the kinematic viscosity can be thought of a diffusion coefficient for velocity. The kinematic viscosity of the fluid thus determines how fast the steady state velocity profile is established:
The larger the kinematic viscosity v (of the fluid) is, the faster the linear steady state velocity profile is reached. If v is small, the flux of momentum is small and the time before steady state is reached is large.
The dynamic viscosity is very temperature and pressure dependent For liquids the dynamic viscosity decreases with increasing temperature while for low density gasses the viscosity increases with increasing temperature. The dynamic viscosity normally increases with increasing pressure.