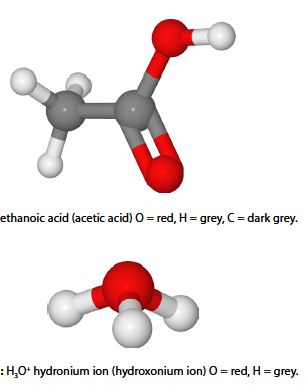
Ethanoic acid (acetic add) is a weak acid which dissociates in water.
CH3 COOH + H2 0 ≈ CH3 C00– + H3O+
An add has an acidity constant Ka which is similar to an equilibrium constant Ka’
Ka’ = [(CH3 C00–) (H3O+)] / [(CH3 C00H) (H2O)]
Where each of the terms in square brackets have been divided by the standard concentration c° = 1 mol L-1 and so the units cancel out to give the pure number, dimensionless “concentrations”. The concentration of the solvent, water, [H2 0] is approximately constant and is incorporated into the acidity constant Ka to give
Ka’ = [(CH3 C00–) (H3O+)] / [CH3 C00H]
Acetic add has an acidity constant Ka = 1.8×10-5. Calculate the hydronium ion concentration [H3O+] for a 0.15 mol L-1 solution of acetic add? We can tackle this chemical problem by saying the fraction of acid dissociated at equilibrium is x. For each molecule of acid that dissociates it gives an equal number of acetate anions and hydronium cations. So at equilibrium the tricky chemical problem has been reduced to solving the quadratic equation using the quadratic formula.
1.8X 10-5 = x2 / (0.15 —x)
Solution
The fraction of acid lost in going to the equilibrium, x, is found by solving the quadratic equation by: (1) multiplying both sides of the equation by the right hand denominator and cancelling out in any single term; (2) multiplying out the bracket;
(1.8 x 10-5) (0.15 —x) = x2 (2.7 x 10-6) – (1.8 x 10-5) = x2
(3) rearranging to the form of a standard quadratic equation; (4) the standard quadratic is solved using the quadratic formula where the symbols have their conventional meanings.
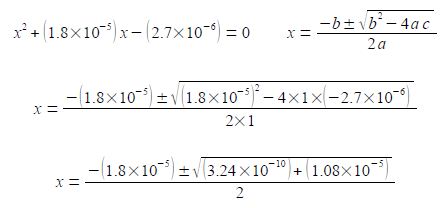
Note the change of sign to the second term within the square root and also the large difference in magnitude between b2 and 4ac. I will temporarily be keeping some extra significant figures in order to show the effect of this relative difference in magnitudes between b2 and 4ac.
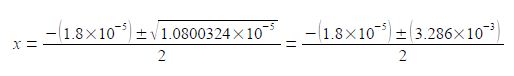
Once we have taken the square root of the second term in the numerator then we only need to retain a sensible number of 4 or 5 significant figures. So which value of x applies in this question? Remember that x is the fraction of acetic acid that has dissociated. A fraction is a positive number of less than one. Another way of looking at this is that you cannot have a negative concentration, thus the chemically correct result is
CH3O+ = x mol L-1 = 1.6 x 10-3 mol L-1
Note: even though some of the data is only given to 2 significant figures it is necessary in order to not lose accuracy in the intermediate steps to carry out the calculation to 4 or 5 significant figures and before the square root is taken to 8 significant figures due to the large difference in the orders of magnitude of b2 and 4ac.
Although not part of the question, for the 0.15 mol L-1 acetic acid solution, this concentration of H3 O+ corresponds to a pH = 2.8.