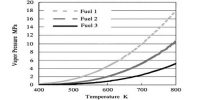
Crude oils often are blended. This is partly because very many are ‘out of spec’ in sweetness (absence of sulphur) and in lightness (reciprocal density). Blending enables an oil as sold to be controlled in these terms, and such a blend will be priced according to how close the sweetness and lightness are to those of one of the benchmark crudes such as West Texas Intermediate, Brent or the OPEC basket.
Application of the Grunberg-Nissan equation for two blended liquids’ to crude oils requires a few approximations to be made. The Grunberg-Nissan equation is:
lnμ12 = x1 lnμ1 + x2 lnμ2 + x1 x2 γ12
where µ denotes dynamic viscosity and x mole fraction, subscripts 1,2 and 12 referring respectively to the two components and to the blend. The parameter γ12 is termed the interaction parameter. In applying to the blending of crude oil we note the following. First as the two oils being blended are both composed of non-polar molecules γ12 can be set to zero.
Secondly, were an average molecular weight to be assigned to each oil and determined (perhaps by freezing point depression of a pure organic liquid) values for the two would not intuitively be expected to differ by much. Mole fractions can therefore be replaced by mass fractions. This gives the simplified form:
lnμ12 = Ф1 lnμ1 + Ф2 lnμ2