Modification of Ideal Gas Equation: Van der Waals’ Equation of State
The ideal gas equation has been derived from the kinetic theory of gases with the help of some simplifying assumptions. van der Waals (1873), a Dutch physicist, pointed out that the following two assumptions of the kinetic theory of gases may not be correct. particularly at high pressures and at low temperatures:
(a) the volume of the gas molecules is negligible compared to the volume of the container.
(b) the molecules do not exert any force of attraction on each other.
van der Waals introduced corrections into the ideal gas equation to account for the above assumptions.
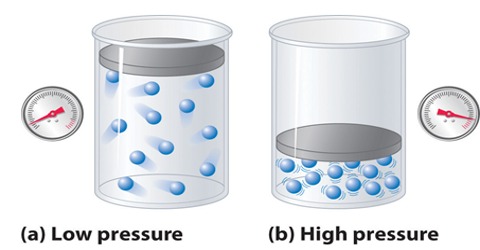
Pressure correction: The facts that gases can be liquefied, and the existence of the Joule-Thomson effect, i.e., the cooling of a gas when forced through a porous plug, indicate that molecules possess attractive forces for one another. These forces, known as van der Waals’ forces, arise from the attractive forces of electrons and protons in one atom or molecule for these in other atoms or molecules. The magnitude of these forces depends, besides other factors, on the distances between the molecules and their masses. When a gas is compressed the molecules get closer to each other and the effect of these forces becomes noticeable. As the temperature is lowered, the molecules become sluggish as their kinetic energy decreases and they have less ability to overcome the attractive forces. At higher temperature the molecules move at higher speeds in a random fashion: although the attractive forces try to draw the molecules together, they stay away from each other because of the motion.
The effect of the attractive forces is that the real pressure P of the gas molecules is less than the pressure they would exert if there were no attraction for one another. Consider a molecule in the interior of the vessel. As this is being acted upon by forces from all directions the total effect is nil. On the oilier hand, a molecule about to strike the wall has its momentum reduced by an unbalanced force trying to pull the molecules towards the interior and away from the wall. The measured pressure is thus lower by a quantity p, than the pressure the puts would exert it ii were ideal. The pressure of the gas, if it were ideal, would then be P + Pa. This is the quantity that is calculated from the kinetic theory.
The quantity Pa may be evaluated as follows: A molecule about to strike the wall will be pulled back by attraction from all the other molecules in the neighborhood; the attractive force will then be proportional to the density, ρ; the number of molecules par unit volume. Again, the average number of molecules which will strike the wall is also proportional to ρ. The total forces trying to pull the molecules about to hit the wall will he proportional to ρ2 or l/V2. Hence Pa = a/V2, where ‘a’ is a constant for the gas.
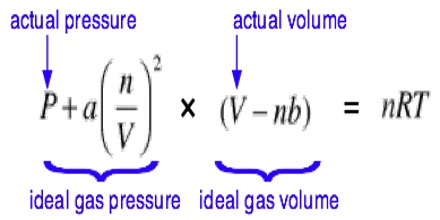
With the introduction of volume correction and pressure correction the gas equation: PV = RT. takes the form;
[P + a/V2] [V-b] = RT
This is known as the Van der Waals’ Equation of state for mole of gas. For ‘n’ moles the equation becomes:
[P + n2.a/V2] [V-nb] = nRT