Chemical spectroscopy and analytical chemistry use light of various types not just visible light but also other regions of the electromagnetic spectrum. The quantum mechanics view of light is that when it is treated as a particle it is made up of a stream of photons. The energy of a single photon, E, is the product of Planck’s constant h = 6.626x 10-34 J s and the frequency of the light v (“nu”).
So this equation combines the particle view of light on the left hand side (the energy of a photon) with the wave view of light on the right hand side of the equation (the frequency of a wave), i.e. this equation embodies wave-particle duality!
E = h v
As mentioned, when light is treated as a wave we have an equation that relates the frequency v and the wavelength λ of light to the velocity of light c.
C = λ v
Where c = 2.998 x 108 m is the speed of light. Combine these two equations and calculate the energy of a single photon of wavelength λ = 427 nm (the symbol nm stands for a unit called a nanometre or 10-9 m).
Solution
C = λ v E = h v
The common variable in these two equations is the frequency, v. The energy of a single photon is found by: (1) rearranging the first equation to get v as the subject; (2) substituting this expression for v into the second equation; and (3) then substituting in the physical quantities.
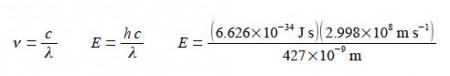
Note that in the calculation we have replaced nanometres by the base units metres in order that the units metres and seconds can cancel out.
E = 4 .652 x10-19 J
This is the energy of a single photon and it is incredibly small, the power of —19 is a very small fraction of a joule. In practice we normally only meet photons in enormous numbers (typically 1023 or more) which can give very large total energies, ≈ 10s of kJ, of light energy.











