One Component Phase Systems: Water System
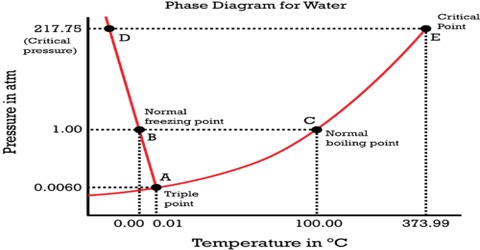
Water can exist in any of the phases – solid (ice), liquid or vapor. All three phases can be represented by the chemical entity H2O. So it is a one-component system. The conditions of equilibria between the various phases of a substance can be represented simultaneously on a single graph which is known as a phase diagram. A system consisting of a pure substance, a one-component system, may be represented by a phase or equilibrium diagram with pressure and temperature as the two axes. Pressure — temperature (p – t) diagram for water is a very simple but important phase diagram that clearly gives us information about equilibrium between different phases, e.g., V ↔ L, L ↔ S, S ↔ V phases. The diagram is shown in the figure.
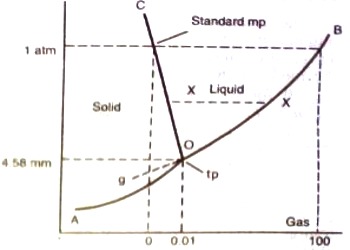
Figure: Phase diagram for water
The different parts of the diagram are:
(a) Carves OB, OC, and OA,
(b) Areas within BOC, to the right of BOA and to the left of AOC
(c) The point O where the three curves OA, OB, and OC meet.
The simplest phase diagrams are pressure-temperature diagrams of a single simple substance, such as water. The axes correspond to the pressure and temperature. The curve OB shows the effect of temperature on the vapor pressure of water. Any point on the curve OB gives the temperature and pressure at which liquid water and vapor co-exist. Since there are two phases in equilibrium the number of degrees of freedom is one (F = 1 – 2 + 2 = 1), i.e., the system is univariant, meaning that any of the two variables temperature and pressure will describe the system. This curse can be extended up to the critical point of water (3740C), because above this temperature no liquid water can exist. The critical pressure is 218 atm. The limit of this curve to the lower temperature side will be the point O, the freezing point of water is shown in Figure. The phase diagram shows, in pressure-temperature space, the lines of equilibrium or phase boundaries between the three phases of solid, liquid, and gas.
Similarly, the system is univariant along with the line OC as any point on the curve gives the temperature and pressure at which solid and liquid water co-exist. The line OC represents the change in the freezing point of water or melting point of ice on changing the pressure. For example, the melting point of ice at 1 atm pressure is 0°C but at a pressure of 133 atm the melting point is – 10C. The melting point of ice is lowered by increasing the pressure, so the curve has a negative slope – an unusual property of water.
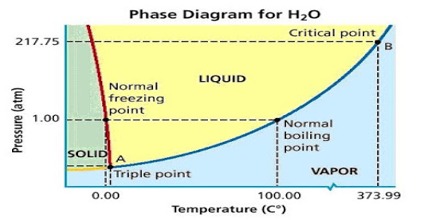
This is because ice has a lower density than that of pure water. The curve OC, therefore, divides the liquid and solid phase – on its right side there is only liquid and on its left there is only solid. This curve theoretically can extend up to infinite pressure. Also along the line OA the system is univariant as any point on the line gives the temperature and pressure at which solid and vapor are in equilibrium. The point on the lines OA and OC can be defined by temperature or pressure curve since there are two phases. The curve OA shows the vapor pressure of ice as a function of temperature. Above this curve there is only a solid phase and below only vapor. This is, therefore, the sublimation curve of ice. The lower temperature limit of this curve is 0 K.
Areas stated in (b) abuse are pure phases, area within BOC describes the liquid phase (water), in the area to the right of BOA water is in the form of vapor and the area to the left of AOC is the region where solid phase (ice) exists. The number of degrees of freedom for the component water in all three regions is two (F = 1 – 1 + 2 = 2), i.e., the system is bivariant in these areas. To describe the system at any point within these regions both temperature and pressure have to be stated.
To summarize, along with OB liquid and vapor co-exist, alone OA solid (ice) and liquid co-exist and along OA solid (ice) and vapor (steam) co-exist. These three curves meet at O. Hence at the point O all three phases solid, liquid and vapor- co-exist or are in equilibrium. This point is called the triple point.
A triple point is, therefore, a point denoted by a definite pressure and temperature at which three phases of a component can co-exist under equilibrium condition.