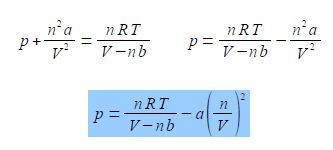The van der Waals equation below models the behaviour of many non ideal gases over wide pressure and temperature ranges.
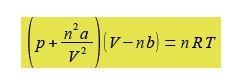
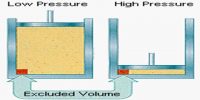
Where p is the pressure; V the volume; T the temperature; n the number of moles of gas; R is the gas constant R = 8.314 J K-1 mol-1; and a and b are constants which have characteristic values for a given molecule. The constant a reflects the attractive London dispersion forces between the molecules, this reduces the pressure exerted on the container walls. The constant b reflects the “excluded volume” of a molecule. All molecules have a certain radius and other molecules cannot occupy the same space, this exduded volume has the effect of reducing the available volume for the movement of the molecules.
Rearrange the van der Waals equation to obtain the pressure as the subject of the equation.
Solution
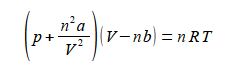
Sequentially:
(1) divide both sides by (V – nb);
(2) cancel out within any single term;
(3) subtract (n2a/V2) from both sides;
(4) and you may want to put the square terms inside a bracket to tidy up the rearranged equation.