Molecularity with Rate-determining Step
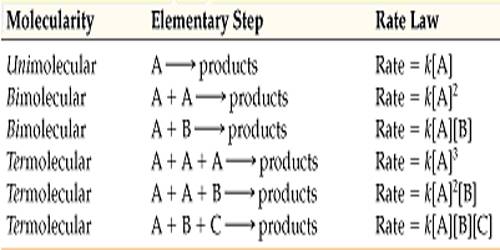
The molecularity is the number of particles (molecules, atoms or ions) on the reactant side of an elementary reaction. We do not talk of molecularity of a net or overall reaction. Molecularity is not related to the stoichiometric equation of a reaction.
If this is the rate law for the rate-determining step, it will also be the rate law for the overall reaction. However, this cannot be the correct one, because the experimental rate law is different. This does not necessarily mean that this mechanism is wrong, but it does mean that the first step is not the rate-determining step. Let us assume that step (2) is the rate- determining step. The rate equation for this step is –
rate = k [A2] [B]
This rate law, however, contains the proposed reaction intermediate (A2), but the experimental rate law contains only the concentrations of A and B. As we will see the concentration of A: cam be expressed in terms of the concentrations of A and B.
Once A2 is formed it can react either of two ways. Since A2 is proposed to be unstable (if it were stable one could isolate it and there would be no question about the proposed steps) it could undergo decomposition to two molecules of A or collide with a molecule of B to give the products C and D. The mechanism proposed should, therefore, include a racism that allows A2 to decompose to two molecules of A.
A2 → 2A
The total steps in the mechanism would then be-
2A → A2 (fast)
A2 → 2A (fast)
A2 + B → C + D (slow)
If the rate at which the intermediate A2 is formed from two molecules of A is the same as the rate at which A2 breaks up form a molecules, then these two reactions form a state of dynamic equilibrium. Because these reactions are much faster than the third step the equilibrium is reached before any significant reaction by the slower step can take place. The first two equations can then be written in the form-
2A ↔ A2
and the total mechanism, in which the first step is an equilibrium, can be written as below:
2A ↔ A2
A2 + B → C + D