Method of limiting density
The methods: Regnault’s method, Dumas method, Hofmann’s method, Victor Meyer’s method, and the buoyancy method are based on the assumption that the vapors behave as ideal gases. Since the equation is not strictly valid for real gases the results obtained are not very accurate. It will be seen that the behavior of real gases approximates to that of ideal gases as the pressure is reduced. This approach towards an ideal state refers only to PV relationships. If the density of gas could be measured at very low pressures, preferably at zero pressure, accurate molecular masses could be obtained. Measurements at very low pressures are beset with experimental difficulties and the error will be large as the densities are so small at low pressures. Limiting density is the density of a gas when the ratio of density per unit pressure is extrapolated to zero pressure, the point at which a gas exhibits ideal-gas behavior. However, the method of graphical extrapolation may be used to obtain accurate values of molecular masses.
In this method, the density (ρ) of a gas is determined at various pressures (P) at constant temperature (T). The values of ρ/P are then plotted against P as shown in Figure. However, the pressure of the gas must he mush below the atmospheric pressure.
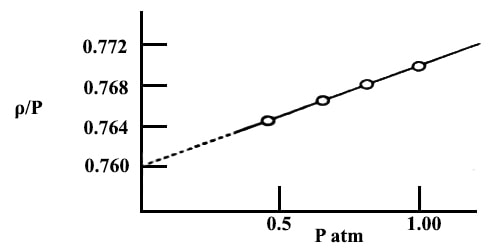
Fig: plot of ρ/P vs P for NH2 gas.
The straight line is extrapolated to the ρ/P axis at zero pressure, the value at this point being designated as (ρ/P). The ideal gas equation then becomes,
M = (ρ/P)0 RT
This is valid for any gas. The molecular mass of the gas may be calculated from the value of (ρ/P)0. In most cases the plot of ρ/P against P is linear. If the plot shows a curvature at higher pressure the straight-line portion may be extrapolated to obtain (ρ/P)0. This method of extrapolation to obtain accurate molecular mass is known is the method of limiting density. The limiting density, ρ0, i.e., the density at zero pressure, however, cannot be obtained by extrapolation of a plot of ρ vs P since the density of the gas vanishes at zero pressure. You’ll notice that volume is a variable in the ideal gas law, but neither density nor mass is a variable. To find density, we have to solve the equation for volume, or V.V = nRT / P. To incorporate mass, we can use the number of moles, or n. The number of moles equals the mass of the gas divided by the molecular mass.
The method which may also be used to determine atomic masses is illustrated in the following example.
Example: The densities, ρ, of NH3 in gas at various pressures, P, and at 0° C are measured. The ratio ρ/P calculated from the data are:
P atm 1.00 0.67 0.50 0.33
ρ/P 0.77169 0.76873 0.76586 0.76385
Calculate the molecular mass of NH3 by the method of limiting density. If the relative atomic mass of hydrogen is taken as 1.008 what is the relative atomic mass of nitrogen?
Solution: A graph is drawn with ρ/P as ordinate and P as abscissa. The points lie on a straight line which, when extrapolated, meets the ordinate at 0.7599.
Hence;
(ρ/P)P→0 = 0.7599
The molecular mass, M = (ρ/P)P→0 RT
= (0.7599) (0.082) (273.1) = 17.01
As the molar formula of Ammonia is NH3, the relative atomic mass of Nitrogen;
= (17.01 – 1.008 x 3)
= 13.99.