Law of Miller indices in Crystal Systems
Crystalline solids exhibit different toms depending on the relative sizes of the ions or atoms, type of binding force, nature of stacking etc. any of the six or sometimes seven main groups into which crystals are commonly classified according to the relative lengths and inclinations of their axes or according to their respective symmetries.
Miller indices
The Miller indices may be defined ‘as the reciprocals of the co-efficient of the intercepts of a given plane on the crystallographic axes, expressed as integers’. The Miller indices may be explained with reference to Figure (intercepts of a crystal plane). If a, b, c are chosen as unit lengths on the three axes, the lengths of the intercepts may be expressed as OA/a, OB/b and OC/c.
The reciprocal of these lengths will then be a/OA, b/OB and c/OC. A consequence of the law of rational indices is that reciprocal intercepts of crystal faces are small whole numbers. Thus if h, k, l are small integers then;
a/OA = h; b/OB = k; c/OC = l
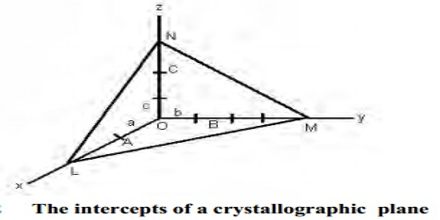
The reciprocal numbers, hkl at are known as the Miller indices. If a face is parallel to any one axis, that is, the length of the intercept is α, the Miller index is reciprocal of α, i.e., 0. The notation is also applicable to planes drawn within the crystal. It is clear that for the standard plane, i.e., the plane which makes intercepts of length a, b and c on the axis, the value of h, k and l are unity. It is often described as a (111) plane. If the intercept of any plane has a negative value it is represented by placing a bar over the Miller index. For example, (111) plane represents a plane which cuts the OZ axis at a distance of – c. The use of the Miller indices may be illustrated with the help of Figure A3 for cubic crystals.
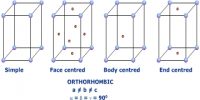
The crystal forms of almost all crystals may be described with the help of seven different sets of co-ordinates. Crystals belonging to any one set are said to form a crystal system. The seven different crystal systems have been illustrated in Figure.
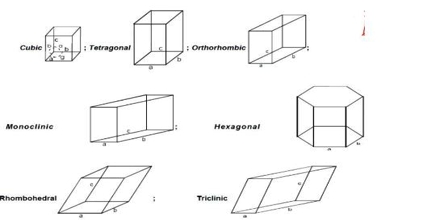
The property which determines to which system a crystal belongs is symmetry. Once a suitable set of axes has been fixed for a given crystal the crystal planes can be described.