The Internal Energy of an Ideal Gas: Joule-Thompson Porous Plug Experiments
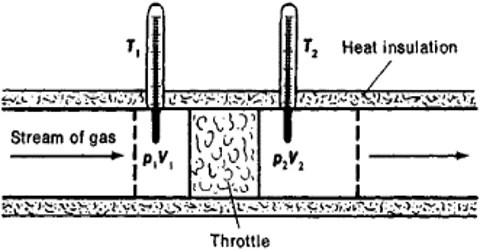
A more refined and sensitive experiment was carried out by Joule in conjunction with William Thomson (later, Lord Kelvin) in order to detect any possible heat effect as a result of free expansion of a gas. In these experiments gas at a high pressure P1 was forced through a throttle valve (originally porous plug) into a space of lower pressure P2. The system was thermally insulated so that, as the gas passed through the plug, no heat could be absorbed or given off. i.e., q = 0. The pressure and temperature on both sides of the plug were measured.
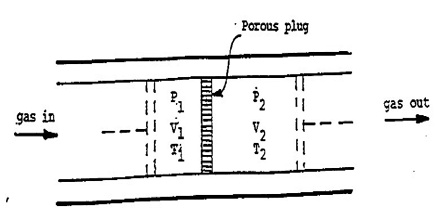
Fig: Joule-Thompson Experiments
It was observed that there was a fall in temperature on the low pressure side when the gas was forced through the plug, i.e., the gas expanded. This cooling effect is known as the Joule-Thomson effect. It may be defined as, “The cooling effect observed when a gas is adiabatically expanded from a high pressure region to a low pressure region through a throttle valve, or porous plug is called Joule-Thomson effect.”
The cooling effect in the Joule-Thomson experiment is attributed to intermolecular attractions of the molecules. An expanding gas has to do work in order to overcome the attractive force so that the molecules may move further apart. The work is done at the cost of internal energy since the process is adiabatic. As a result the temperature of the expanding gas will fall.
Subsequent experiments demonstrated that under ordinary conditions the cooling effect was observed with must gasses except hydrogen and Helium, which registered an increase of temperature in the Joule-Thomson experiment. If however, the experiment with these gases were performed at a very low temperature the cooling effect was observed as with other gases. It was, thus, established that for each gas there is a temperature above which heating is observed in a Joule Thomson experiment, whereas below this temperature coolers is noticed. Thus temperature is known as the Joule-Thompson inversion temperature (or simply inversion temperature). For hydrogen and helium the inversion temperatures are considerably below the room temperature. Hence these gases undergo heating on adiabatic expansion under ordinary conditions of temperature.
It can be shown that the enthalpy of gas on the two sides of the porous plug in the Joule-Thompson experiment is the same, i.e., to say that the Joule- Thomson experiment is isenthalpic. If P1 and V1 are the pressure and volume of the gas before passage through the plug and P2 and V2 are the corresponding quantities after passing through the porous plug the work of expansion is given by;
w = P2V2 – P1V1 … … … (1)
We know the equation, ∆U = q – w
or, ∆U = q – (P2V2 – P1V1) … …. ….. (2)
But, ∆U = U2 – U1 and q = 0, so, equation (2) becomes,
U2 – U1 = 0 – (P2V2 – P1V1) = – (P2V2 – P1V1)
or, U2 + P2V2 = U1 + P1V1
and, H2 = H1 … … … (3)
The result of Joule-Thompson Experiments are expressed in terms of the Joule-Thompson coefficient defined by,
μJ,T = (δT/δP)H … …. ….. (4)
The quantity μJ,T is thus defined as, “the change in temperature in degrees when the pressure is changed by one atmosphere under conditions of constant enthalpy.” Three cases may be considered:
(i) μJ,T is positive, then T decreases when P decreases, and the gas cools upon expansion.
(ii) μJ,T is negative, then T increases when P decreases, the gas is heated up upon expansion.
(iii) μJ,T = 0, the gas is neither heated nor cooled upon adiabatic expansion, μJ,T = 0 only when dT = 0 for any value of dP.
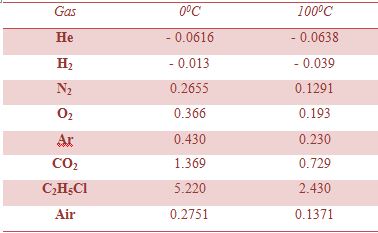
Most common gases, except He and H2 have positive μJ,T at room temperature (Table) and thus will cool during Joule-Thompson expansion that starts at room temperature.
Table: Joule-Thompson co-efficient at 1.0 atm for gases (Unit: K atm-1)