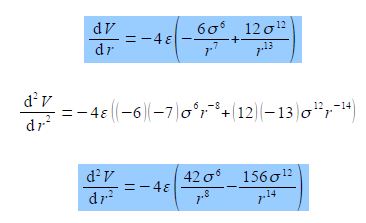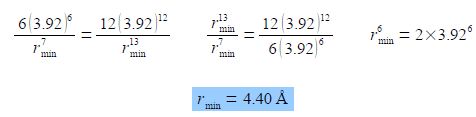V = – 4 ε [(σ/r)6 – (σ/r)12]
Question 1: The variables in the Lennard-Jones equation are V and r, Firstly, find the derivatives of V with respect to r dV/dr. Secondly, differentiate the first derivative with respect to r to find the second derivative d 2V/dr2 for the interaction between N2 molecules.
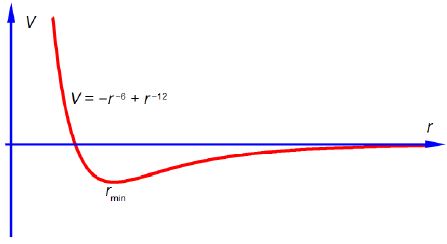
Question 2: Use the solutions of Question 2 to find the separation at which the Lennard-Jones potential V is at a minimum, that is the distance between two N2 molecules at which the potential energy is a minimum.
Solution 1:
Bring the denominators of the pair of inner brackets up to the numerators before differentiating.
V = – 4 ε [(σ/r)6 – (σ/r)12];
V = – 4 ε [(σ6r-6 – σ12 r-12]
(dV/dr) = – 4 ε [- σ6r-6 – (- 12) σ12 r-13]
Solution 2:
To find the separation at which the potential V is at a minimum we use the first derivative. Leaving a in angstroms will give r in angstroms. For clarity I have not shown the units in this evaluations of the equation.
(dV/dr) = – 4 ε [(6 σ6/r7) + (12 σ12 / r13)]
Either 4ε must equal zero, which it cannot, or the term in brackets equals zero giving the following,
Rmin = 4.40 A is the separation of two N2 molecules at the minimum potential energy (see below Fig) and is larger than the 3.7 A “hard sphere” intermolecular interactions diameter of N2.