Ammonia is an important industrial chemical.
Ammonia, N= Blue, H= Gray
Ammonia is synthesized using the equilibrium reaction where the reactant and products are in the gas-phase.
N2 + 3 H2 ≈ 2 NH3
Its makes sense to use the partial pressures of the gases to define an equilibrium constant Kp. The reaction of forming ammonia from its elements has an equilibrium constant of Kp = 977 at a particular temperature.
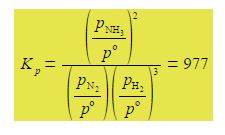
Kp is given in terms of the partial pressures of the reactants and products in pascals where each partial pressure is divided by the standard pressure of p° = l x 105 Pa = 1 bar and thus Kp is dimensionless. Each of the terms is raised to the power of its stoichiometric coefficient. Because the standard pressure p° = l x 105 Pa each of the p° terms affect the value for Kp and we cannot make a simplification similar to the one we made for Kc but each of the Kp equations must be written in full with the p° values included.
For our reaction we initially have 1.00 x 105 Pa pressure of N2 and 3.00 x 105 Pa of H2 which are mixed, there being no NH3 present and the mixture is allowed to come to equilibrium. If x is the fraction of a mole of N2 which is lost due to the reaction then the equilibrium constant becomes
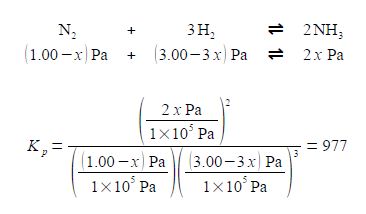
Note that each time the reaction “occurs” we form two molecules of NH3 hence the term 2x. Likewise, each time the reaction occurs we lose 3 molecules of H2 thus the term in the bracket is (3.00 — 3x). Within each of the bracketted terms the units Pa cancel out so this is written as
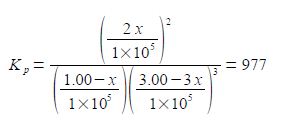
Firstly, calculate the fraction by solving for x using the quadratic formula. Secondly, using this value for x calculate the partial pressures of all the reactants and products. We can simplify the equation by taking out the common factors.
Solution
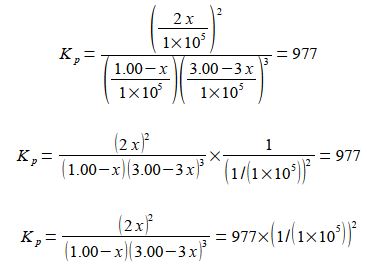
The equilibrium equation may be solved for x by:
(1) taking out the common factor of (1.00 – x) in the denominator and also squaring in the numerator;
(2) collecting the (1.00 – x) common factors together;
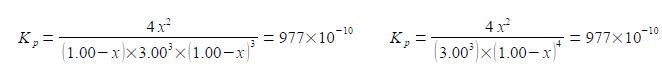
(4) cubing the 3.00 and rearranging the numerical factors;
Kp = 4/27 [x2 / (1-x)4] = 977 x 10-10 kp = (27 * 977) / 4 x 10-10
(5) square rooting both sides of the equation;
x / (1 – x)2 = √ {(27 x 977) / 4} x 10-10 = 81.2081 x 10-5
(6) rearranging by multiplying by the denominator on both sides of the equation, then cancelling terms; (7) squaring the bracket; (8) multiplying out the bracket;
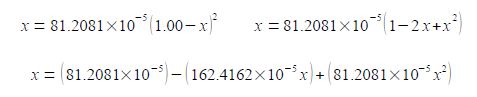
(9) rearranging into the “standard” quadratic form, note that “162” has become “163”; and (10) dividing by 81.2081 x 10-5 throughout to make the coefficients much more manageable.
(81.2081 x 10-5 x2) – (162.4162 x 10-5 x) + 81.2081 x 10-5 = 0
x2 – 2.0123x + 1 = 0
We can solve this quadratic equation using the quadratic formula,
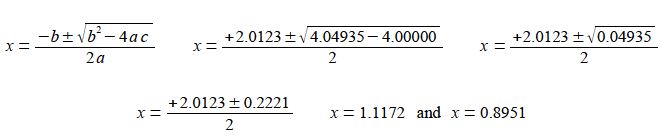
As the mole fraction must be positive and less than one then x = 0.8951 is the chemically correct result. This gives the three equilibrium partial pressures as













