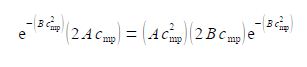Explain Maxwell Boltzmann Distribution of Speeds of Gas Molecules

The fraction of identical molecules in a gas with speed c (ignoring the direction of the velocity) is f(c) and is given by the Maxwell Boltzmann distribution of speeds.

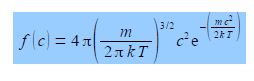
Where m is the molecular mass in kg; k is Boltzmann’s constant which is the gas constant per molecule k = R/T = 1.3807 x 10^-23 J K^-1; and T the temperature of the gas in K. Thus the Maxwell-Boltzmann distribution is isotopic composition dependent. We are now going to use a common trick which helps us see the wood from the trees. The first two terms are constant at a given temperature. So we can make the equation look less daunting by calling them a constant A. Secondly, we see that at a constant temperature the exponential term becomes exp(—Bc²) where B = m/2kT. At constant temperature we have the equation.

f (c) = A c² e^-bc2

Firstly, sketch the plot of the above f(c) versus c equation. Secondly, by differentiating the equation with respect to c show that the graph has a maximum at c_mp = (2kT/m)^1/2 which can be identified with the most probable speed of a molecule, c_mp.

Here,

f (c) = A c² e^-bc2

We see that the equation is the product of two terms in c, The first, c², makes f(c) increase from zero upwards with increasing c. The negative exponential term makes f(c) decrease from 1.0 downwards towards zero with increasing c. So the fraction f(c), the product of these two terms, will start from zero for c = 0, then drop back to zero at large values of c and for intermediate values of c the fraction will pass through a maximum value. Below Figure shows the two constituent curves in red and the product of them in blue.

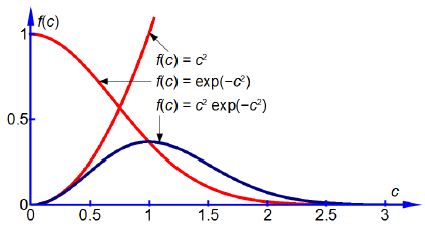
The maximum is when df(c)/dc = 0 and we need to differentiate the equation. Let y = Ac² and x = exp( – Bc²) so that f(c) = xxy and use the rule for the differentiation of a product of two functions.

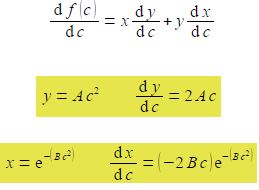
dx/dc has come from using the general form of the differential of an exponential power term

de^u/ dx = [du/ dx] e^u

Therefore from the differentiation of a product of two functions we have the following

d f (c)/dc = e^-bc2 (2 Ac) + (Ac²) (- 2Bc) e^-bc2

Therefore when df(c)/dc = 0 we can find the maximum in f(c) which gives the molecular speed at the maximum i.e. the most probable speed cmp.