Arrhenius equation is used to calculate the rate of a reaction. It is an important part of chemical kinetics. It helps in understanding the effect of temperature on the rate of a reaction.
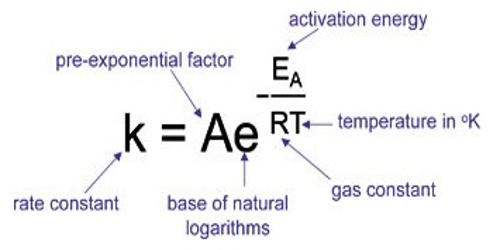
This equation was proposed in 1889 by Svante Arrhenius. The rate constant k for a chemical reaction is related to the temperature T by the Arrhenius equation.
k = Ae– (Ea/RT)
Where k = Rate constant
A = Frequency factor
Ea= activation energy
R = gas constant
T = Kelvin temperature
Here, A and Ea are constants for a given chemical reaction; R is the gas constant R = 8.314 J K-1 mol-1; and T is the absolute temperature in K. For a particular biochemical reaction k= 20 L mol-1 s-1 when T = 300 K. If Ea = 50 kJ mol-1 for this reaction, by differentiating the Arrhenius equation with respect to T, find the change in the value of k when T increases by 1 K to 301 K. Remember to use the base unit of Ea = 50000 J mol-1 in the calculation and not its multiple of KJ mol-1.
Here,
k = Ae– (Ea/RT) ;
(20 L mol-1 s-1) = Ae– [(50000 J mol-1/(8.314 JK mol-1)(300K)]
A = 1.017 x 1010 L mol-1 s-1
Let x = 1/T, then dx/dT = – T-2 and so,
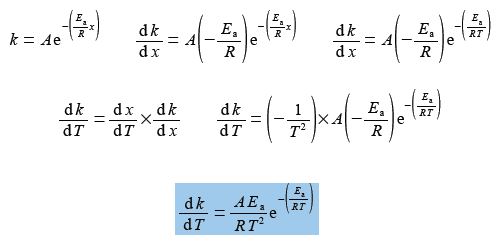
Treating the differential as separable terms and substituting the values for the variables with dT = 1 K gives
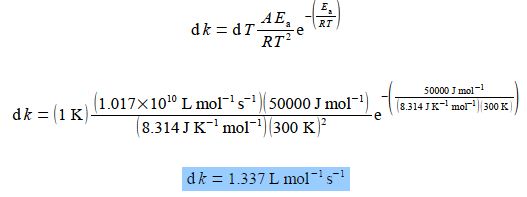
The basis of the Arrhenius equation is the collision theory. According to this theory, a reaction is a collision between two molecules (of the same substance or of two different substances) to form an intermediate. This intermediate so formed is unstable, which exist for a short period of time. The intermediate breaks to give two molecules of the product. The energy used in forming the intermediate is known as the activation energy.