[B] = [A]0 [k1 /(k2 – k1) (e-k1t – e-k2t)
By consideration of each of the terms of the equation find approximate expressions for [B] and d[B]/dt when k1 is very much larger than k2 i.e. k1 >> k2.
When k1 >> k2 then the following approximations may be made for negative exponential functions. The condition (k1 >> k2) means k1 is much larger than k2 and thus exp(—k1 t) ≈ 0 and as k2 is small and positive then exp(—k2 t) ≈ exp(0) ≈ 1 and (k2 — k1) ≈ k1.
[B] = [A]0 [k1 /(k2 – k1) (e-k1t – e-k2t) ≈ [A]0 [A]0 [k1 / -k1] (0-1) ≈ [A]0
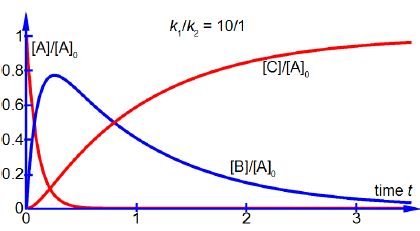
As [B] ≈ [A]0 over part of reaction time, see below Figure, the final product concentration [C] does not start to increase appreciably until the intermediate concentration [B] has passed its maximum by which time the reactant concentration [A] in negligible in chemical reactions. Using the same approximations as above with the equation for the rate of forming the intermediate d[B]/dt we have
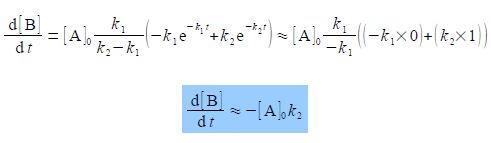
Over much of the reaction the rate of change of the intermediate concentration d[B]/dt to form the product C will approximately depend on the rate of the slow “Rate Determining Step” k2.