A conjugated molecule (also called a polyene) is one with alternating single and double carbon-carbon bonds in its backbone.
Linier conjugated molecule, H= gray, C= Dark gray
These molecules are important biologically for many functions including your ability to detect light within your eyes’ retinas and for plant photosynthesis. Polyenes are also important industrial dyes. The quantum mechanics equation for the π-electrons in a “linear” conjugated polyene molecule has a wavefunction ψ(x) that depends upon the position x along the length, L, of the molecule. The ideas of wavefunctions and quantum mechanics for such systems are covered early on in your Chemistry degree. The general equation that applies to all wave motion is given below.
ψ(x) = A cos (kx) +B sin (kx)
Where A, B and k are constants whose values need to be determined for the linear conjugated molecule. Find the constant k and any constraints that A or B may have using the following two boundary conditions. Firstly, when x = 0 then ψ(0)= 0 and secondly, when x = L then ψ(L) = 0.
Solution
ψ(x) = A cos (kx) +B sin (kx)
The sin and cos are in radians. At the left hand end of the polyene molecule where x = 0, ψ(0) = 0 but we have cos(0) = 1 and sin(0) = 0. So the sine function fits with the quantum mechanics but the cosine does not. Hence in order to remove the cosine term from the general wave equation we must set A = 0. The general wavefunction becomes modified to
ψ(x) = B sin (kx)
At the right hand end of the polyene molecule where x = L, ψ(L) = 0 and so sin (kL) = 0.. This means kL must be equal to it or an integral number n of π where n = 1, 2. 3, is a quantum number. In general, quantization arises because of the fulfilling of “boundary conditions” such as the ones in this question. We rearrange the sine angle equation kL = nπ to give the value of the previously unknown constant k.
kL = nπ
k = nπ / L
Finally we have the wavefunction for the particle (the π-electrons) in a 1-dimensional box (the polyene conjugated molecule).
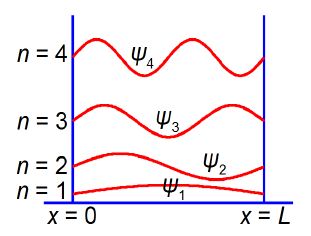
ψ(x) = B sin (nπx / L)
We have found the constants A = 0 and k = nπ / L and the only constant that has yet to be found is B. The value of the constant B is calculated, and below Figure shows the shape (and the relative energies) of the wavefunctions for a particle in a 1-dimensional box.