Experimental Determination of γ of a Gas
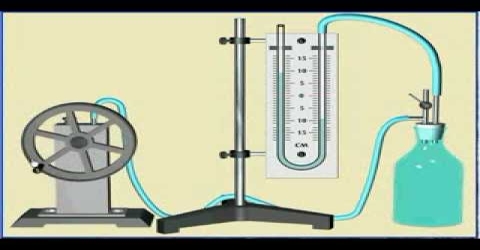
(a) F. Clement and C. B. Desormes used the principle of adiabatic expansion to determine the value of γ. The gas at a pressure greater than one atmosphere is placed in a large vessel (capacity 30-40 L) fitted %3/4 nth a rubber stopper and water or an oil manometer (Figure).
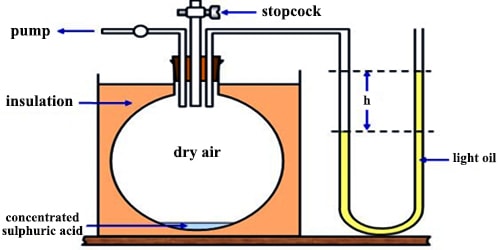
Fig: Clement and Desorme apparatus
The pressure P1 is measured. The stopper is suddenly opened and then closed again. The pressure of the gas momentarily becomes equal to that of the atmosphere and during the expansion, which is virtually adiabatic, the gas is cooled. As it warms up again and attains the temperature of the surrounding, the pressure rises to P2. Let V1 be the volume of one mole of gas at pressure P1 and V be the volume after adiabatic expansion when the pressure is P. For an ideal gas.
P1V1γ = PVγ … … … (1)
The initial and final temperatures are the same, the final pressure is P2 and the corresponding volume of one mole of gas is V. It follows by Boyle’s law, that,
P1V1 = P2V2 … … … (2)
From the equation 1 and 2, one can obtain;
(P1/P2)γ = P1/P
or, γ = (log P1 – log P) / (log P1 – log P2)
The ratio of the specific heats may thus be calculated.