Equation of a Perfect gas
Let pressure, volume and temperature of a given mass of an ideal gas be respectively P, V and T. From Boyle’s law we get, V ∞ 1/P (when temperature T is constant.)
Again, from Charles’s law we get,
V ∞ T, (when pressure P is constant)
Combining these two laws we get,
V ∞ T/P (when T and P, both are constants)
or, V = K T/P
or, PV / T = K
or, PV = KT … … … (1)
Now, at temperature T1, T2, … …, Tn, the pressures and volumes of that gas are respectively P1, P2 … …, Pn and V1, V2, … …, V3. Then from equation (1) we get,
P1V1/T1 = P2V2/T2 = P3V3/T3 = … … = PnVn/Tn = K = Constant
K is a gas constant and P, V and T are called the elements of state of a gas. The value of K depends on the mass of a gas. It is proportional to the mass of the gas. Now, from Avogadro’s hypothesis, 1 mole of any gas contains the same number of molecules under identical conditions of temperature and pressure. If we consider one gm-molecule or I mole of the gas then K as designated by R. The value of R is same for all gases. For this reason R is called universal gas constant or molar gas constant.
So, for 1 mole of any gas,
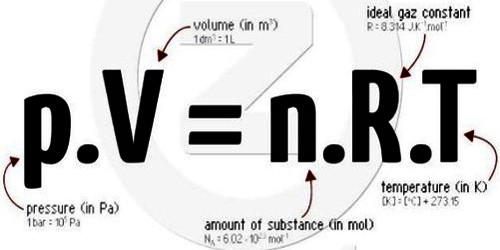
PV = RT
and for it mole gas, PV = n RT … … … (2)
Now, if any two of three quantities; P, V and T are known, the third can be found out by the above equations.
Equation (2) is the general equation of an ideal gas. It is also called the combined equation of Boyles and Charles’s laws.
Again, if ‘m’ be the mass of the gas of molecular weight M,
then, n = m/M. So equation (2) can be written as,
PV = n RT = m/M RT
It is the ideal gas equation or equation of state of gas.