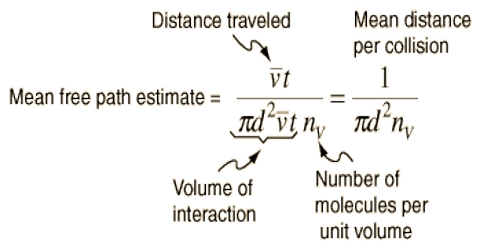
The mean free path is the standard distance an element traverses before it experiences a clash. Pressure, temperature, and a few other factors affect solidity can obliquely affect mean free path.
Effect of pressure and temperature on the value of the mean free path
(a) Effect of pressure: For is given the quantity of gas n, i.e., the number of molecules per unit volume, the mean free path decreases with an increase of volume (i.e. decrease of pressure) so that increases with the decrease of pressure.
The sum of the impulses imparted by all the molecules to the wall is, in effect, the pressure. For an exacting time scale, an element travels larger distances before the collision as the volume is implicit to be stable.
In rising pressure –
- It will augment the mean free path of the molecules in a gas sample.
- It will reduce the mean free path of the molecules in a gas sample.
- It will have no consequence on the mean free path of the molecules in a gas sample.
(b) Effect of temperature: Again for a given quantity of gas when the temperature is increased at constant pressure the volume Increases Hence the ‘n’, the number of cat molecules in unit volume, decreases. From the expression above with decrease of n, the value of l increases.
So, as the temperature increases → the Kinetic energy of the molecules increases → the Faster motion of molecules takes place within a similar time interval.
In increasing temperature –
- It will augment the mean free path of the molecules in a gas sample.
- It will reduce the mean free path of the molecules in a gas sample.
- It will have no consequence on the mean free path of the molecules in a gas sample.
Therefore, Mean free path increases with raise ‘Temperature’. But, the order of proportionality varies depending on the type of particle. However, raising the temperature would augment the collision rate or the mean free time.
Example: Calculate the mean free path of nitrogen molecules at 1.0 atm pressure and 25°C. Collision diameter for nitrogen is 3.50 x 10-8 cm.
Solution: It is necessary first to calculate the number of molecules per cubic centimeter.
Volume of 1 mole of gas at 250C = (22,414/273.16) x 298.16 ml = 24474 ml.
n = [6.02×1023/24474] = 2.46×1019
We know
l = [(1/√2) x 1/(πσ2n)]
= [(1/√2) x [1/(3.142).( 3.50 x 10-8).( 2.46×1019)]
= 7.5×10-6
At 1 atm pressure and 250 C the value of l is of the order of 10-5 cm. At a pressure of 10-5 atm, therefore, the mean free path becomes about 1 cm.