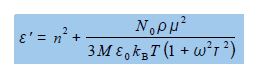An alternating electric field of frequency w has an electric field, E = Ec, exp(iɷτ), which varies with time τ (“tau”). Applying an alternating field to a dilute solution of polar molecules allows you to measure the effect of the solvent with the polar molecules in the solution. This solvent effect is called the dielectric constant Ԑ of the solution at the frequency ɷ of the applied field. For example, water which is very polar has a dielectric constant of 80.10 at 20°C but n-hexane which is very non-polar has a dielectric constant of 1.89 at 20°C. This information is of great value in deciding which solvent(s) to use in designing separation methods, for sample preparation and in the chromatography techniques used in analytical chemistry.
The dielectric constant of a solution is,
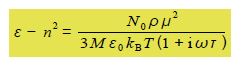
The dielectric constant Ԑ is a complex number and is conventionally written as,
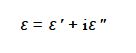
The parameters n, No, ρ, M, Ԑo, μ, kB, are all constants at a constant temperature T. Experimentally we measure the real part of the dielectric constant e so rewrite the above equation to determine the real part Ԑ’ of this complex dielectric constant.
Solution
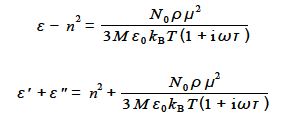
Consider the term 1/(1 + iɷτ) as it is the only term containing i and the rest of the terms on the right hand side are just constants. The 1/(1 + iɷτ) term is division by a complex number and when we multiply it top and bottom by the complex conjugate of the denominator and simplify we find the real part of this is,
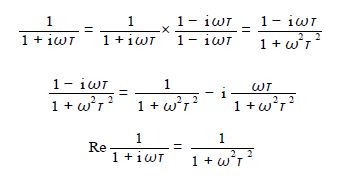 So the real part of the original equation can be rewritten, see below, and it is this part of the dielectric constant of the battery polymer electrolyte that is measured experimentally.
So the real part of the original equation can be rewritten, see below, and it is this part of the dielectric constant of the battery polymer electrolyte that is measured experimentally.