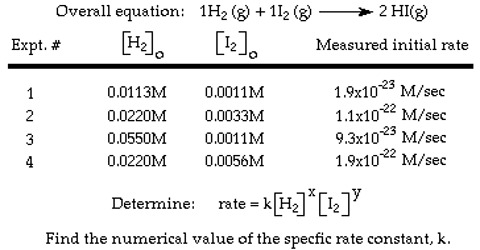
Determination of rate law: Initial rate method
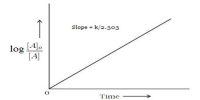
The method consists in carrying out several experiments for the same reaction in which the starting or initial concentration of the reactant is different. In each experiment the concentrations of the reactant at different times are determined and the data are plotted as concentration versus time as shown below in Figure.
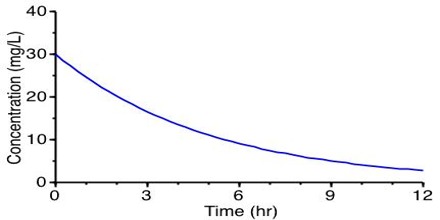
Figure: Concentration vs time
A tangent to the curve at the initial concentration is drawn and the gradient of the tangent gives the initial rate. The initial rates for different concentrations are compared from which the order of the reaction can be determined.
In cases where the rate depends on the concentrations of more than one reactant, for example A and B, two or more experiments are done in which the concentration of one of the reactants, say A, is kept constant while the initial concentration of B is different. Again two or more experiments are done in which the concentration of B is kept constant while the initial concentration of A is different. The subsequent procedures are the same as in the example.
An illustration of such case is given below.
Example: In a series of experiments between nitric oxide and bromine
2NO (g) + Br2 (g) → 2 NOBr2 (g)
carried out at 273°C the following data were obtained:
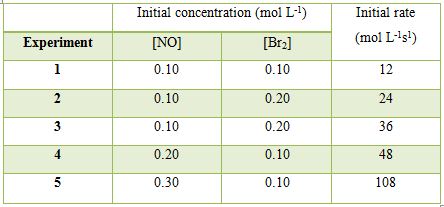
Determine the rate law for the reaction and calculate the rate constant.
Solution: Since there are two reactants we can tentatively write the rate equation as follows:
rate = k [NO]m [Br2]n
In experiments 1 to 3 the concentration of NO is kept constant and concentration of Br2 is varied. When the concentration of Br: is doubled (experiments 1 and 2) the rate becomes double; when the concentration of Br2 is made three times (experiments 1 and 3) the rate also becomes three times. This can only be explained if the rate is directly proportional to the concentration of Br2 or the order with respect to Br2 is one.
Similarly, comparing experiments 1 and 4, when the concentration of Br2 is kept constant but that of NO is doubled the rate becomes four times. Again comparing experiments 1 and 5 when the concentration of Br2 is kept constant and the concentration of NO is increased by a factor of 3 the rate increases 9 times. These lead to the conclusion that the order with rasped to NO is 2.
Therefore,
rate = k [NO]2 [Br2]
The rate constant can be calculated using the data for any one of the experiments,
From the data for experiment 1 we get,
12 mol L-1s-1 = k (0.10 mol L-1)2 (0.10 mol L-1)
Solving for k, we have,
k = (12 mol L-1s-1) / (0.10 mol L-1)2 (0.10 mol L-1)
= 1.2 x 103 L2 mol-2s-1