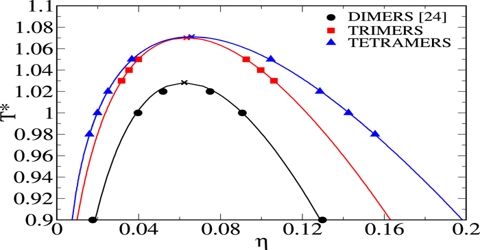
The critical volume is more difficult to determine. It is obtained with the help of a rule known as the law of rectilinear diameter discovered by Cailletet and Mathias (1886). The law states that the mean value of the densities of liquid and saturated vapor for a stable substance, measured at the same temperature, is a linear function of the temperature. The measurement of critical volume is very hard because it varies significantly for the slightest dissimilarity of temperature and pressure near the critical section; hence for the measurement of critical volume, the material must be kept in a completely critical temperature and pressure.
If ρm is the mean of the densities at a temperature T, then,
ρm = ρ0 + α T … … … (1)
where ρ0 = density at T = 0 and α is a constant.
The critical volume is the volume at Tc and Pc. In spite of the standard physical state at regular conditions, it is calculated as (Zc*R*Tc)/Pc, where Zc is the critical compressibility aspect, which ranges from 0.2 to 0.3. The value of Zc is often given in the literature; it can be estimated with low accuracy. No help can be obtained by the usual equations of state, mostly the cubic ones. In fact, the critical volume has little real use.
This law holds fairly accurately for a number of substances but is not strictly true in all cases. The applicability of the law of Cailletet and Mathias is illustrated in Figure; for CO2 (from Amagat’s data). The curses AC and BC represent densities at the liquid and vapor respectively at different temperatures. The two curves when extended meet at C which is the critical temperature. The mean densities fall on the line CD, this shows the validity of the law.
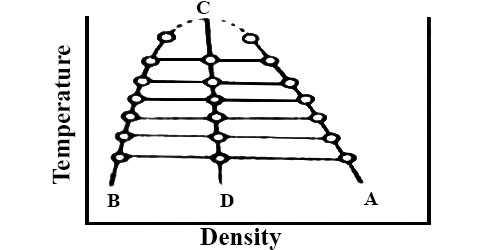
Fig: T vs ρ showing the validity of the law of rectilinear diameter
To determine the critical volume of the substance the densities of liquid and vapor are measured at different temperatures near the critical temperature. These are then plotted as is Figure. The mean of the densities at the same temperature is then calculated and the mean values at different temperatures are joined by a straight line. The straight line is now extended and the mean density at the critical temperature is obtained from the graph. The critical volume (Vc) per gram of the substance is equal to the reciprocal of the mean density (ρc) at the critical temperature. i.e.
Vc = 1/ρc
The densities of the liquid and the vapor at a given temperature are obtained as follows: A known mass of liquid is taken in a graduated scaled tube and its temperature raised to the desired value. The mass is given by
m = ρ1V1 + ρgVg
where ρ1 and V1 are the density and volume of the liquid phase and ρg and Vg are the corresponding values for the vapor phase, the volumes being read off the graduations. A different mass of liquid is similarly heated to the same temperature and the corresponding volumes of liquid and vapor measured. From the two simultaneous equations obtained by substituting the experimental quantities in the above equation, ρ1 and ρg at that temperature may be obtained.