The non-bonding interaction between two neutral atoms or two neutral molecules, their intermolecular interactions, is given by the Lennard-Jones equation.
V = – 4 ε [(σ/r)6 – (σ/r)12]
Where V is the potential energy of the interacting molecules, r is the distance between the two molecules and e is the depth of the potential well. the 6th power term describes the long-range attraction between the molecules due to the van der Waals or dispersion forces. The 12th power term represents the short-range repulsion between the molecules from the overlap of their electron orbitals when the distance between the molecules becomes so small that they are essentially in contact. For the interaction between two N2 molecules the constants are ε = 765 J mol and σ = 3.92 x 10-10 m. Sketch the shape of the graph for this potential.
Here,
V = – 4 ε [(σ/r)6 – (σ/r)12]
To sketch the above equation we can simplify it to V = – Ar6 + Br12 and separately plot the shape of r-6 and r-12 and then “add” their shapes to arrive at the final shape of the graph as shown in below Figure. The position of the minimum and its depth depend upon the values of A and B (that is upon the values of ε and σ). The – Ar6 term being negative decreases the potential as the molecules get closer, they are attracting one another due to the van der Waals forces. The power of – 6 in – Ar6 acts at longer range than the ± Br-12 term. The + Br-12 term is effective at short range and increases the potential as the distance decreases and the molecules increasingly repel one another.
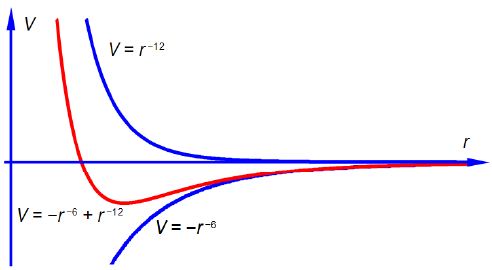
sketch of V = r6 , V = r-12 , combine plot of V = – r6 + r-12