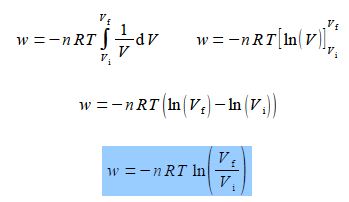In Chemistry it is very common to have gases being formed, reacting, compressed or expanding. A simple way of understanding such processes is to begin with a “mechanical” picture of a gas trapped inside a cylinder by a piston, below Figure.
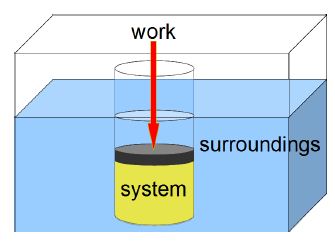
The gas is called “the system” in thermodynamics and everything other than the gas is called “the surroundings”. If the pressure of the system p is the same as the surroundings and the volume of the system is V then the work done on the system (gas) is given the symbol w. As the gas expands at constant temperature, T, the work done on the system (the gas) is shown in the equation below.
W = – ʃ p d V
The negative sign arises because as the system expands then dV > 0 and the gas does work on the surroundings, pushing the surroundings back. As w is the work done on the system then it will be negative in this case as in expanding, the gas is doing the work! Assuming for the moment the gas is an ideal gas then from the Ideal Gas Law we can obtain the integral below where n is the number of moles of gas in the system and R is the gas constant, R = 8.314 J mol-1 K-1.
pV =nRT
p = nRT / V
W = – ʃ [nRT / V] d V
Find the work done when the expanding gas expands from an initial volume Vi to a final volume Vt by integrating this equation.
So,
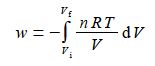
Taking the constants outside the integral for clarity, the temperature of the expanding gas T of the gas is constant and the number of moles of the system n is constant (gas in neither formed or lost), we may now integrate.