Cubic Lattices
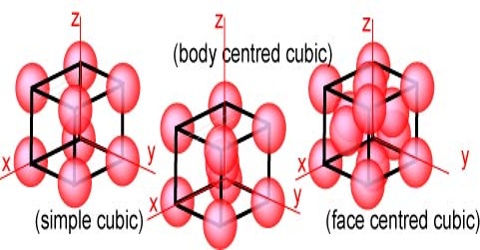
In the cubic lattice system the three different space lattices are called the simple cubic, the face-centred cubic and the body-centred cubic lattices. In the simple cubic lattice the structural units are at each corner of the unit cube. In the face-centered lattice there is one unit at the centre of each face, in addition to those at the corners. Body-centered lattice is distinguished by having one unit at the centre and one at each corner of the unit cube. The three types of reflecting planes in each of the three lattices are shown in Figure.
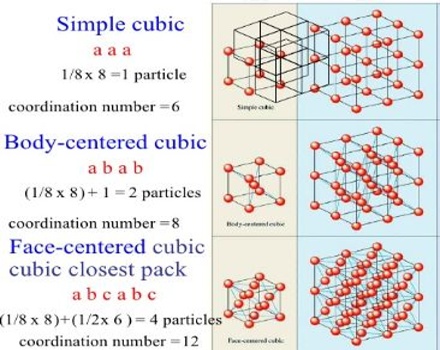
Figure: Plane through cubic lattices (a) simple cubic, (b) body-centred cubic and (c) face-centred cubic.
The distance between the planes (hkl) in a cubic lattice may be shown to be given by;
dhkl = [a / (h2+k2+l2)1/2] … … … (1)
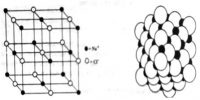
where a is the length of a side of a unit cube. The distances between planes in the three lattices may be noted in Figure 1.
When equation (1) is combined with the Bragg equation, we obtain;
Sin2θ = (λ2/4a2) (h2+k2+l2) … … … (2)
Thus the angle at which reflections from different planes (h k l) and hence maxima in the plot of intensity vs. 2θ would be calculated from equation (2). Conversely, the maxima obtained experimentally may be used to determine the planes from which the reflections are obtained. For a cubic lattice the following spacing are allowed:

It should be noticed that the term 7 is missing since there is no set of integers such that (h2+k2+l2) = 7. The ratios of dhkl values of each cubic structure are given in Table.
Table: Ratio of dhkl values for different structures