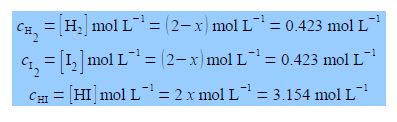H2 + I2 ≈ 2 HI
The above chemical reaction when carried out at a temperature of 425°C has the I2, HI and H2 all in the gas phase. The chemical symbol of the two half-arrows indicates that the reaction is at a dynamic equilibrium going in both directions simultaneously. This reaction has an equilibrium constant KC of 55.64 at 425°C.
KC = [HI]2 / [H2] [I2] = 55.64
If we originally placed 2 mol L-1 of H2 and 2 mol L-1 of I2 in a flask at 425°C with no HI present, calculate the equilibrium concentrations of H2, 12 and HI when equilibrium is achieved at this temperature? The way we tackle this type of question is to assume that x moles of H2 and I2 are consumed in going from the above original conditions to equilibrium and 2x moles of HI are formed when equilibrium is achieved. The concentrations at equilibrium are then
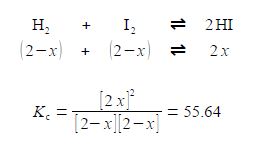
The rather difficult Chemistry problem comes down to solving the Maths for x in this equation. Solve this equation in the most efficient manner which may not necessarily be by the use of the quadratic formula. Then using the chemically sensible value of x from your solution, work out the equilibrium concentration calculations for the three molecules.
Solution
Note that the HI concentration 2x is all squared, it is not 2x2. Writing the denominator as a square term allows us to then take the square root of both sides.
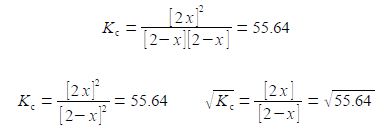
This is solved by: (1) multiplying left and right of the equals sign by [2 — x] and cancelling out within a single term; (2) then multiplying out the bracket;
(2x) / (2-x) = 7.459; (2x) = 7.459 * (2-x) or, (2x) = 14.918 – 7.459x
(3) taking 7.459x over to the left hand side: (4) finally solve for x. In this example the two roots of the quadratic are the same so there is no choice for the “chemically sensible” root.
2x + 7.459x = 14.918 9.459x = 14.918 so, x = 1.577
Thus the final equilibrium concentrations are