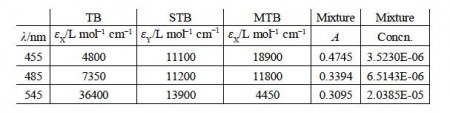
A student in their lab dass measured the following spectroscopic data for some pure samples of three indicators thymol blue (TB), semithymol blue (STB) and methylthymol blue (MTB), below Figure.
Rewrite the data in matrix form and by appropriate matrix manipulation; find the concentrations of TB, STB and MTB in the mixture. You should attempt the manual approach which we have used up until now and find the difficulties involved.
Solution
This is the same fundamental problem as above, extended to a ternary mixture. It is assumed that the concentrations of the dyes are low and their absorbances at a range of wavelengths are additive, i.e. they are each dominant in at a given wavelength and they don’t interact chemically with one another. First let us try the manual matrix approach.
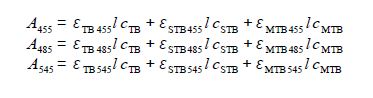
Writing this in matrix form, entering the student’s lab results (without units for clarity) and then rearranging the matrix equation into the standard simultaneous equations form we have

but trying to solve this manually gives us problems, here is the determinant
|A|= +4800(11200 x 4450- 11800 x 13900)- 11100(7350 x 4450- 11800 x 36400) +18900(7350 x 13900- 11200 x 36400)- 7350(11100 x 4450- 18900 x 13900) +11200(4800 x 4450- 18900 x 36400)- 11800(4800 x 13900- 11100 x 36400) +36400(11100 x 11800- 18900 x 11200, 13900(4800 x 4450- 18900 x 36400)+4450(4800 x 11200- 11100 x 7350)
The above determinant is awful! The manual method of matrix algebra for this type of numerical matrix equation has been useful for initial learning purposes also for small 2×2 matrices and matrices with “sparse” numbers. The manual method is also useful for examination questions where computers are not allowed! However, the manual method is a problem when finding the determinant and the matrix of cofactors for 3×3 or larger matrices and for those with numerically “rich” matrices as in the one above. It is slow, clumsy and prone to errors. Lees see how easy it is to use a spreadsheet and the inversion of matrix A. and then directly use x = A-1 b which is shown in below figure.
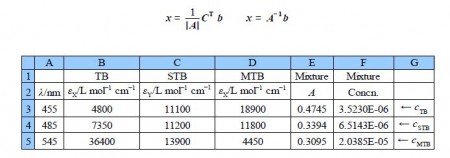
The wavelengths are not used in the calculation, they are just helpful reminders. The matrix A is in the array B3:D5 and the matrix b is in array E3:E5. We select the three empty cell F3:F5 and type in the formula window the following array formula
=MMULT(MINVERSE(B3D5),E3:E5)
Do not press enter or return as it is an array function rather than a simple Maths function. Instead on a PC press Shift+Control+Return or on Mac Command+Return and the solution appear in the array F3:F5. The spreadsheet commands are MMULT for matrix multiplication the two matrices. The first matrix is the inverse of A (Le. A-1) MINVERSE and the second is the absorbances of the mixture, b.
cTB = 3.52 x 10-6 mo1 L-1
cSTB = 6.51 x 10-6 mo1 L-1
cMTB = 2.04 x 10-5 mo1 L-1