In uniform circular motion, the object travels with constant speed v along a fixed circular trajectory with radius r. The speed and radius determine the period of the motion, i.e., the time to complete one full revolution:
V = (circumference / period) = (2πr / T), so, T = (2πr / V)
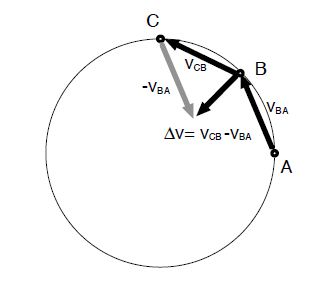
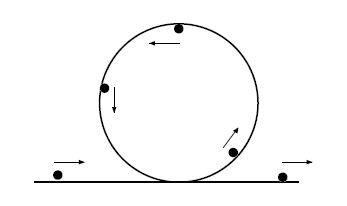
We gain insight by considering a numerical example. An object is moving on a circle with radius R = 8.0 cm. The object is at point A at time t = 0, at point B at time t = 2.0 s, and at point C at time t = 4.0 s• The vectors representing the average velocities during the intervals [0, 2 s] and [2 s, 4 s], VBA and VCB , respectively, can be drawn, and the difference vector be found by geometric construction,

Thus, the acceleration is directed towards the center, so that the net force acting on the object must be directed towards the center as well.
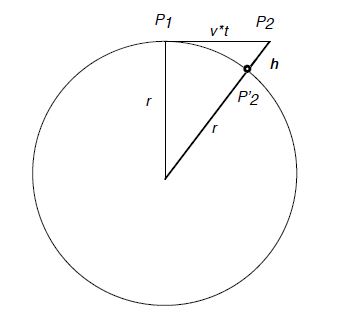
We find an expression for the magnitude of the acceleration. At time t = 0, the object is at point P1 moving with a velocity v in tangential direction. At time t, the object would be at point P2. Instead, it moves along the circle, and thus is at point P2 . We find an expression for the height using Pythagorean theorem: r2 + (vt)2 = (r + h)2.
We assume that the time interval is short, so that vt < r and h < r.
Since (r + h)2 = r2 + 2rh + h2 ≈ r2 ± 2rh, we simplify the RHS: r2 – (vt)2 ≈ r2 ± 2rh so that h = (vt)2/2r = 4 (v2/r)t2. We compare the RHS with x = at2/2, and find the value of the centripetal acceleration:
ac = (v2/r)
For the numerical example above, we find v2/r ≈ (3 cm/s)2/(6 cm) = 1.5 cm/s2, in agreement with the graphical method.
We find the force acting towards the center from Newton’s second law:
Fnet = mac = m (v2 / r)
This is sometimes called “centripetal force;” however, there is no new force involved, and the centriptal force is the net force.