When a ball bounces off a wall, it is reflected with the same speed but travels in the opposite direction: v → -v The kinetic energy is constant, and the net work is done on the ball by the wall is zero. Since Δv = vf – vi = -2v = aave Δt, we define the impulse as force * time,
J = F Δt ….. ……….. ……(1)
So the momentum of an object with mass in as mass * velocity is
p = mv ……. …….. ……(2)
Newton’s second law, F = ma , can then be written,
J = Δp ……. …….. ……(3)
This relationship is somewhat analogous to the work-kinetic energy theorem. It allows us to describe changes in the velocity of an object without knowing details of the forces [the magnitudes and direction and for how long they last]. For the ball bouncing off the wall, we do not know the magnitude of the force exerted by the wall on the ball or the duration of the force; however, the impulse of the force has a known value, J = – 2mv. The unit of momentum and impulse are [J] = [p] = N • s = kg • m/s.
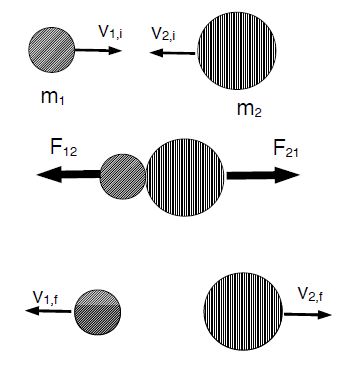
We have two objects [pucks] sliding on (idealized) ice and traveling at velocities v1,i and v2,i respectively. They collide and exert forces F12 and F21 on each other. These two forces are an action-reaction pair so that F12 = – F21. After the collision, they travel at velocities v1f and v2f. Note that there no external forces, for example the gravitational force in the case when the surface is inclined.
We have for the impulses,
F12 Δt = m Δv1 = m1 (v1,f — v1,i)
F21 Δt = m Δv2 = m2 (v2,f — v2,i)
Newton’s third law states F12 = -F21, or F12 + F21 = 0, so that the addition of the two equations yields
(F12 + F21) Δt = m1 (v1,f — v1,i) + m2 (v2,f — v2,i) = 0 or,
m1 v1,i + m2 v2,i = m1 v1,f + m2 v2,f
We define the total momentum of the system [mass m1 and mass m2],
ptot = m1 v1 + m2 v2
We thus see that the total momentum is the same before and after the collision. We say that the total momentum is conserved. No detailed knowledge of the forces is necessary.