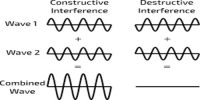
In physics, when two sets of waves of the same frequency and same or nearly equal amplitude travelling through the same medium overlap, then it is found that due to superposition, they wholly or partly multiply each other at certain times and places and reinforce each other to produce a greater effect at other time and places. This phenomenon is called interference.
Interference is a characteristic feature for all waves, independent of the nature of the wave, and explains several wave phenomena: (1) standing waves that are relevant for waves along a string and the sound waves and (2) diffraction.
We assume that two coherent sources S1 and S2 (indicated by the two dots) produce waves in the same region. Coherent means that successive crests [solid] and troughs [dotted] of the two sources are produced at the same time. The addition of two waves follows the superposition principle. When two or more waves are present simultaneously at the same location, the resultant disturbance is the sum of the disturbances from the individual waves; that is, we add the amplitudes and not the intensities from different sources.
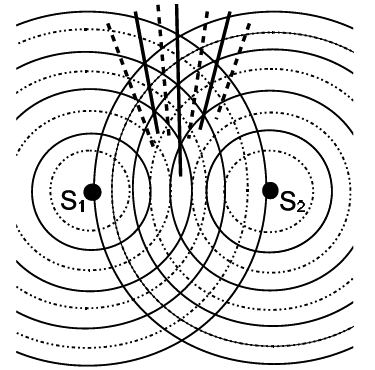
In the forward direction, a crest (trough) from S1 ‘meets’ a crest (trough) from S2. Along with this (solid) centre line, a wave with amplitude 2A develops: we say that the waves add constructively. The direction of the centre line defines the zeroth-order maximum. On either side of this line, two dotted lines connect dots, where a crest (trough) from S1 meets a trough (crest) from S2: we say that the two waves add destructively, i.e., they cancel out each other. The directions of these two lines define the first-order minimum. We then indicate with solid lines the points, where a crest (trough) from S1 meets a crest (trough) from S2. These lines define the first order maximum.
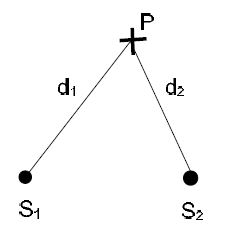
The condition for a maximum depends on the distances d1 and d2 between the two sources S1 and S2 and the observation point P: ׀d1-d2׀ = n λ, n = 0, 1, 2, …
so that n = 0 for the zeroth-order maximum defines the center line. For the minimum, we have ׀d1-d2׀ = (n + 1/2 ) λ, n = 0, 1, 2, …
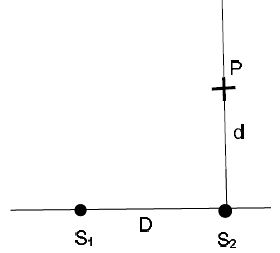
Example: Two speakers vibrate in phase and produce the sound with frequency f = 440 Hz [musical tone “Al. The speakers are separated by the distance D = 23 cm. Find the shortest perpendicular distance from the speaker S2, where the sound from the two speakers cancels. What is the distance to the next maximum?
Solution: We find the wave length of the sound λ = (345 m/s) /(440 m) = 0.78 m. Since n = 0, distance d1 follows from Pythagorean theorem: (λ/2)2 = D2 + d12 so that
d1 = √ (0.78 m/2)2 – (0.23m)2 = 0.32 m.
We set n = 1 and find the distance to the first maximum:
d2 = √ ((0.78 m)2 — (0.23 m)2) = 0.75 m.
The distance between maximum and minimum is Δd = d2 – d1 = 0.44 m.