The velocity of the mechanical wave depends on the elasticity and inertia of the medium.
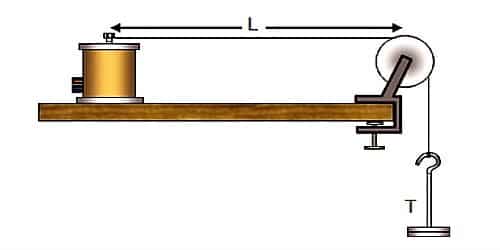
We can create a transverse wave on a stretched string. The speed of a wave depends on the distinctiveness of the medium. The speed of transverse wave set up in the string depends upon numerous factors like tension applied (T), mass per unit length of the string, etc. For example, in the case of a guitar, the strings vibrate to construct the sound.
The velocity of a transverse wave along a stretched string
Let consider a string filled at one of its ends and tension be applied at the other end. When the string is plucked at a point, it begins to vibrate. Consider a transverse wave proceeding from left to right in the form of a pulse when the string is plucked at a point as shown in Figure.
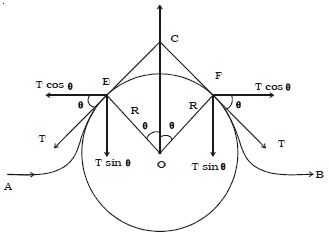
EF is the displaced position of the string at an instant of time. It forms an arc of a circle with O as center and R as the radius. The arc EF subtends an angle 2θ at θ.
If m is the mass per unit length of the string and dx is the length of the arc EF, then the mass of the portion of the string is m dx.
Centripetal force = (m.dx.v2)/R
This force is along CO. To find the resultant of the tension T at the points E and F, we resolve T into two components Tcosθ and T sinθ.
T cosθ components acting perpendicular to CO are of equal in magnitude but opposite in direction, they cancel each other.
T sinθ components act parallel to CO. Therefore the results of the tensions acting at E and F is 2 T sin θ. It is directed along CO. If B is small, sinθ = θ and the resultant force due to tension is 2Tθ.
resultant force = 2Tθ
we know, 2θ = dx/R
so, 2T (dx/2R) = T (dx/R)
For the are EF to be an equilibrium,
(m.dx.v2)/R = T (dx/R)
So, v2 = T/m
Or, v = √( T/m)
Speed of a transverse wave in a stretched string –
The speed of the waves on the strings and the wavelength verify the frequency of the sound produced. The strings on a guitar have dissimilar width but might be made of comparable material.
Consider a stretched string and if given crosswise interruption on one end then the fracas travels all over the string. Thereby giving rise to transverse waves. The particles move up and down and the waves travel at right angles to the vacillation of the particles. Hence the velocity of a transverse wave along a stretched string is in a straight line proportional to the square root of tension in the string and inversely proportional to the square root of linear density.
Transverse wave speed determined by:
Mass per unit length – As mass gives increase to Kinetic energy. If no mass then no kinetic energy. Then there will be no velocity. It is denoted by μ.
Tension -Tension is the key feature which makes the fracas propagates along the string.
Because of tension, the disturbance travels throughout the wave. It is denoted by T.