Velocity of the artificial satellite
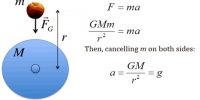
Suppose the height of a satellite is h from the surface of the earth and if R is the radius of the earth, then the radius of the orbit of the satellite will be r = R + h. The gravitational attraction of the earth provides necessary centripetal force on the satellite for its rotation. So, if the velocity of the satellite is v, GMm/r2 = mv2/r. Here M, m are respectively the masses of the earth and the satellite,
v2 = GM/r
or, v = √(GM/r)
= √ [(GM)/(R + h)] … … … (1)
Time period of the satellite: If the time period of the satellite is T, i.e., if the time to revolve around the earth once at a height h from the surface of the earth is T, then its linear velocity will be,
v = [2π (R + h)] / T
so, [2π (R + h)] / T = √ [(GM)/(R + h)]
or, T = [2π (R + h)] [√ (R + h) / GM] … … … (2)
Height of the satellite: Suppose the height of the artificial satellite from earth’s surface = h, then by squaring both sides of equation (1) we get,
T2 = [4π2 (R + h)3] / GM
or, (R + h)3 = GMT2 / 4π2
so, h = [GMT2 / 4π2]1/3 – R.