Use of Kirchoff’s Law in Wheatstone Bridge
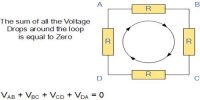
Kirchoff’s Law states that the algebraic sum of currents at a junction of an electric circuit is zero. The concept of the laws Current and resistance in a simple circuit can be determined by using Ohm’s law. But if the circuit is complex then Ohm’s law is not sufficient. For this reason, Kirchhoff’s two laws are used to calculate current and resistance in a complex circuit. Kirchhoff’s Laws for current and voltage lie at the heart of circuit analysis.
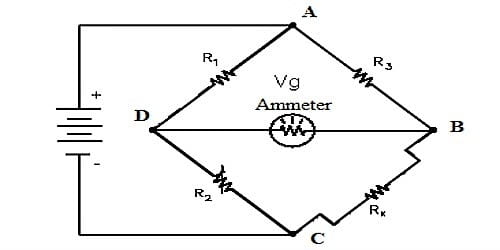
If four junctions are made due to the formation of a closed loop by connecting four resistors in series and if an electric cell is connected between the two opposite junctions and a galvanometer is connected between the other two opposite junctions then the circuit thus formed is called Wheatstone bridge.
Let us consider that four resistors P, Q, R, and S are arranged like tetrahedral ACDF. Wheatstone bridge is formed by connecting a battery B or an electric source, a plug key K and a variable resistor X between the junctions A and D and a galvanometer G between the junctions C and D [Figure].
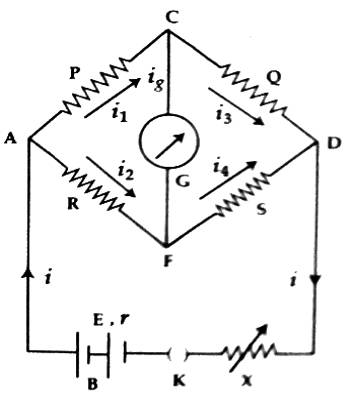
In this situation, the main current ‘i’ entering the network at A divides and flow through different resistors of the network and meet again at D. Whether current through the galvanometer will flow or not depends on the potentials at points C and F. If for the resistances the potentials at C and D are not equal, then current will flow through the galvanometer and the galvanometer will give some deflection. This situation is called unbalanced condition. But if the potentials at points C and F are equal, then no current flows through the galvanometer and the galvanometer shows no deflection. This condition is called balanced condition or null condition. By controlling different resistances in the circuit, the balanced condition is established.
Wheatstone bridge is an electrical circuit, which is used for the correct measurement of the resistance of a conductor. Wheatstone bridge applications are used to sense electrical and automatic quantities. This bridge circuit is used to compute the unidentified resistance values and as a means of an amendable measuring instrument, ammeters, voltmeters, etc. But, the simple Wheatstone bridge application is light measurement using a photoresistive device.
In the Wheatstone bridge circuit, a light dependent resistor is positioned in the place of one of the resistors. But, the current digital millimeters offer the easiest method to analyze a resistance. Balanced bridge circuits are used in numerous electronic applications to determine changes in the strength of light, strain or force. In recent days, Wheatstone bridge is used in numerous applications such as; it can be used with present op-amps to crossing point various sensors and transducers to amplifier circuits. The dissimilar types of resistive sensors which can be used in a Wheatstone bridge circuit include potentiometers, LDR’s, strain gauges and thermistor’s, etc. The Wheatstone bridge circuit can be used in a number of applications and nowadays, with presently equipped amplifiers we can use the Wheatstone Bridge Circuit to interface various transducers and sensors to these amplifier circuits.