Torque or Moment of a Force
A rigid body can rotate about a point. For example, a photograph can rotate about the point of contact between the nail and the thread from which the photograph is hanging and rotating; besides, the wheel of a vehicle can rotate about its axis.
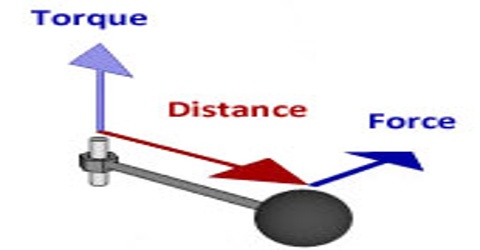
Torque is a force acting perpendicular to the line connecting the point at which it acts to the pivot point, where F is the magnitude of the force acting on the object and d is the perpendicular distance from the pivot point to the force. The torque or moment of force about a chosen axis is the product of the force and its moment arm. It is denoted by τ (Tau).
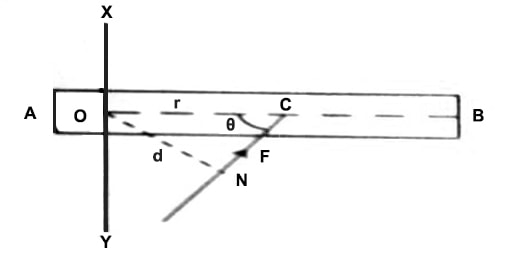
Explanation: Let us consider a thin sheet AB fixed in horizontal position in such a way that it can rotate about point 0 and about the perpendicular axis XOY [Figure]. If the sheet is rotated by applying a force at any point, say C, it is observed that,
- Greater the magnitude of applied force, greater is the power to rotate.
- Greater the distance d between point O and the point of application of force F, the greater is the power to rotate.
- If the line of action of the force is parallel to the plane of the sheet, it will not rotate.
Because of the above reason, the magnitude of the moment of force or torque is measured by the product of the magnitude of the force and the perpendicular distance d of the action of force from the axis of rotation.
τ = d x F
or, Torque or Moment of Force = Force x Perpendicular distance.
In fig, from O distance of the point of action of the force, F = r, the line of action NC of the force = d and NCO = θ.
So, ON = d = r sin θ
then, τ = d x F = r F sin θ
In vector form τ can be expressed as, τ = r x F
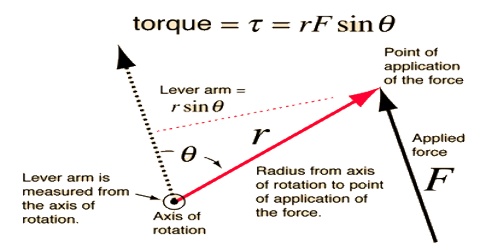
Here r and F are respectively position vector and applied force. The direction of τ is perpendicular to the plane containing r and F. For anti-clockwise rotation, the direction of τ is upward and its value is positive; whereas, for clockwise rotation, τ is downward and its value is negative.
According to the equation, τ can be defined as:
Definition: For an object moving about an axis, the cross-product of the position vector of the point where the force is applied and the force is called torque.
Unit of torque or moment of a force: S.I. unit of τ is Newton-metre (N-m).
Dimension: We know, τ = force x distance = MLT-2 x L = [ML2T-1]