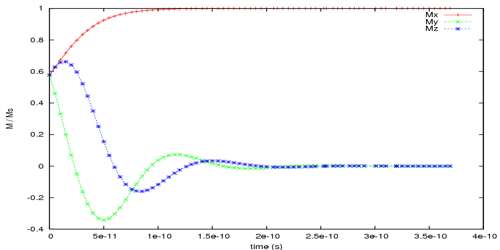
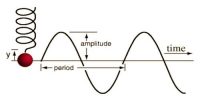
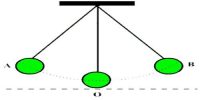
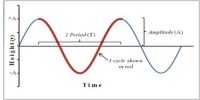
Spacial periodicity
If the time period is with respect to space or position, then it is called spacial periodicity. For example, the time period of a simple pendulum is different at different places of the earth. From simple harmonic motion, it can be shown that its time period,
T = 2π√(L/g), here L = length of the pendulum and g = acceleration due to gravity.
Since the value of ‘g’ is different at different places of the earth and also above and below the earth’s surface, hence time period also varies accordingly. This is spacial periodicity.
The introduction of a characteristic spatial length scale, or consistently a spatial frequency, is a big covenant, because when other spatial length scales in the physical structure correspond with that one, there can be big consequences. For example, when the wavelength of x-rays or electrons or neutrons is some integer harmonic of the (projected) lattice spacing, then waves scattered from subsequent (or every second or every third, etc.) plane of atoms will interfere constructively – this is called the Bragg condition, is what gives diffraction patterns that have verified so practical in characterizing material structures.